Одноканальная двухфазная система массового обслуживания с отказами с разной производительностью приборов, страница 9

,                                                                       (4)

,                                                                                 (5)

к которым следует добавить нормировочное уравнение

.                                                                (6)

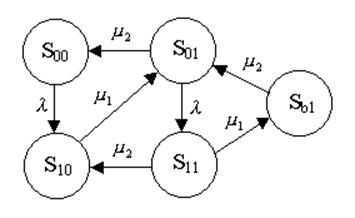           Рисунок 6 – Граф переходов системы с блокировкой

Аналитический расчет

Обозначим:

A = = 7,7

B =  =2,8

C = =2,139

В результате получаем:

,

,

.

Решение данной системы уравнений будем искать по правилу Крамера:

P₀₁ = ,   P₁₀ = ,   P₁₁ = .

Здесь  определитель системы

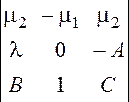 =   = 140,856

 определитель для P₀₁:

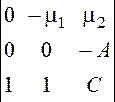 = =31,57

 определитель для P₁₀:

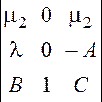 = =34,92

 определитель для P₁₁:

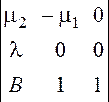 = =8,2

Таким образом, получаем:

·  Вероятность того, что занят обслуживанием только первый прибор:

P₀₁ =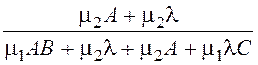=0,224

·  Вероятность того, что занят обслуживанием только второй прибор:

P₁₀ =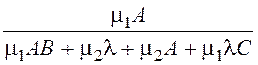=0,248

·  Вероятность того, что заняты оба прибора:

P₁₁ =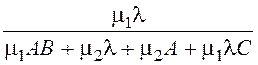0,058

Вероятность того, что оба прибора свободны:

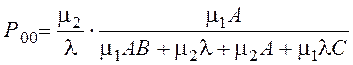=0,403

Вероятность блокировки первой фазы:

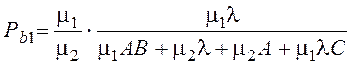=0,066

Определим относительную и абсолютную пропускные способности системы.

Первый прибор отказывает заявке в обслуживании, если он занят обслуживанием другой заявки, а занят он в состояниях S₁₀ и S₁₁ и S_b1, поэтому:

 =0,628

Абсолютная пропускная способность первого прибора равна:

 =1,256

относительная пропускная способность второго прибора равна 1

.

Абсолютная пропускная способность второго прибора и системы в целом равна:

= 1,256

Программа

lambda  equ  2;

mu_1   equ  4.1

mu_2   equ  3.6

*

tab_T_syst          table m1,0,2,15; Таблица интервалов времени

*                                    нахождения заявок в системе

tab_TQ_bloc         qtable Q_bloc,0,1,15; Таблица интервалов времени

*         блокировки (нахождения заявок в очереди из-за блокировки)

*

                    generate (exponential(1,0,(1./lambda)))

*

                    TEST E (F1&~F3&F2),1,MET1

                    SAVEVALUE 4+,1; Подсчет блокировок (b1)

*

MET1      TEST E (F1&F2),1,MET2

                    SAVEVALUE 3+,1; Заняты обе фазы ((11) или (b1))

*                   (первая фаза либо обслуживает, либо блокирована)

MET2      TEST E (~F1&~F2),1,MET3

                    SAVEVALUE 10+,1; Обе фазы свободны (00)

MET3      TEST E (F1&~F2),1,MET4;

                    SAVEVALUE 1+,1; Занята только первая фаза (10)

MET4      TEST E (~F1&F2),1,MET5

                    SAVEVALUE 2+,1; Занята  только вторая фаза (01)

*                   Подсчет потерь

MET5      TEST E F1,1,MET6; если первая фаза занята, то отказ

                    savevalue POTERI+,1; Подсчет потерь

                    terminate  ; Удаление потерь

*

MET6      split 1,MET7; Создание одной копии транзакта

          savevalue 100,(exponential(2,0,(1./mu_1))); задание

*                   времени задержки в первой фазе и в приборе дублёре

*

          seize 1; Начало обработки заявки в первой фазе

          advance x100

*

                    QUEUE  Q_bloc ; Очередь из-за блокировки

                    GATE NU  2; БЛОКИРОВКА

                    DEPART  Q_bloc

*

          release 1; Завершение обработки заявки в первой фазе

*

          seize  2; Начало обработки заявки во второй фазе

          advance  (exponential(3,0,(1./mu_2)))

          release  2; Завершение обработки заявки во второй фазе

*

                    tabulate  tab_T_syst

                    terminate  ; Удаление обслуженных заявок

*

MET7      seize  3; Дублёр первой фазы без блокировки

          advance  x100

          release 3

          TERMINATE ;  Удаление копий

* 

*         Задание времени моделирования

                    GENERATE 100000

*         Определение характеристик системы

          SAVEVALUE  P_00,(x10/n1);

          SAVEVALUE  P_10,(x1/n1)

          SAVEVALUE  P_01,(x2/n1)