Одноканальная двухфазная система массового обслуживания с отказами с разной производительностью приборов, страница 4

                    2    SAVEVALUE            1             0       0

                    3    SAVEVALUE            1             0       0

                    4    SAVEVALUE            1             0       0

                    5    SAVEVALUE            1             0       0

                    6    SAVEVALUE            1             0       0

                    7    TERMINATE            1             0       0

SAVEVALUE               RETRY       VALUE

 P_SUM                    0          1.000                           

 Q_1                      0          0.672                           

 Q_2                      0          0.698                           

 A_1                      0          1.344                           

 A_2                      0          0.938                           

FEC XN   PRI         BDT      ASSEM  CURRENT  NEXT  PARAMETER    VALUE

     2    0          20.000      2      0      1

График.

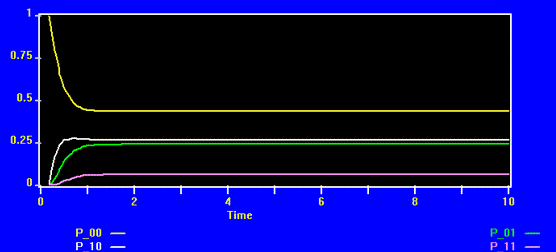
Все полученные путём моделирования характеристики занесём в таблицу и сравним с данными аналитических расчётов:

Характеристика системы	Данные аналитических расчётов	Данные, полученные при интегрировании	Величина отклонения от данных аналитических расчётов, %	Данные моделирования	Величина отклонения от данных аналитических расчётов, %
P00	0,432	0,432	0	0.434	0.46
P10	0,266	0,266	0	0.266	0
P01	0,240	0,240	0	0.239	0.42
P11	0,062	0,062	0	0.061	0.16
Q1	0,672	0,672	0	0.673	0.15
A1	1,344	1,344	0	1.345	0.13
Q2	0,698	0,698	0	0.700	0.29
A2	0,938	0,938	0	0.941	0.32

Вывод:  Из таблицы видно, что величины отклонений не превышают 1%, следовательно система смоделирована правильно.

Система без потерь

Имеется одноканальная двухфазная система массового обслуживания без потерь, состоящая из двух приборов разной производительности (рис. 3).

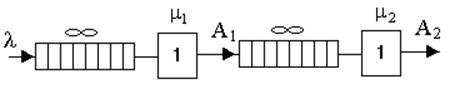
Рисунок 3 – Структурная схема системы без потерь

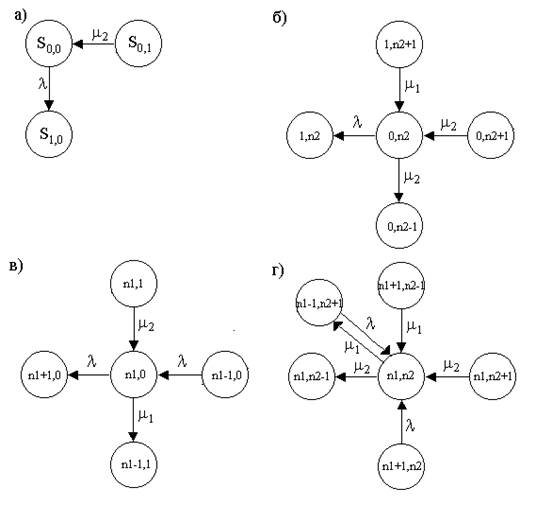
Рисунок 4 – Фрагменты графа переходов системы без потерь

На рис. 4 показаны наиболее важные фрагменты графа, по которым можно написать уравнения состояний системы

. . .

. . .

. . .

Аналитические расчеты.

Так как потерь нет ни в первой, ни во второй фазе, то относительные пропускные способности фаз равны 1:

q₁ = 1 и q₂ = 1.

Поэтому абсолютные пропускные способности фаз равны

 = 2   (A₁ – это интенсивность заявок на входе второй фазы).

 = 2

для каждой фазы получаем:

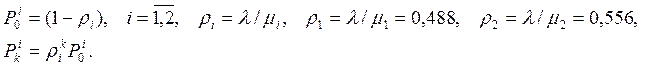
Высчитывать все возможные состояния слишком долго и нецелесообразно, поэтому для примера рассчитано несколько состояний.

P¹₀=0.512 – первая фаза свободна

P²₀=0.444 – вторая фаза свободна

P¹₁=0,488*0,512=0.25 – занято первое устройство, очередь свободна.

P²₁=0,444*0,556=0,247 – занято второе устройство, очередь свободна.

P₂¹=0,1219 – в первой фазе две заявки

P₂²=0,137 – во второй фазе две заявки

* и т.д.

*

*

Здесь i– номер фазы, k – число заявок в фазе.

Общая вероятность того, что первая фаза занята, а вторая свободна получится:

P2=p₁*p²₀=0.488*0.444=0.217

Общая вероятность того, что вторая фаза занята, а первая свободна получится:

P3=p₂*p²₀=0.556*0.512=0.285

Для вероятностей различных состояний системы получаем:

§  Вероятность того, что оба прибора (обе фазы) свободны от заявок

§  Вероятность того, что в первой фазе находится i заявок, а во второй j заявок