Используя формулу производной частного, получаем
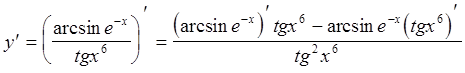 .
.
Далее, используя формулу производной сложной функции и соответствующие табличные производные, получаем:
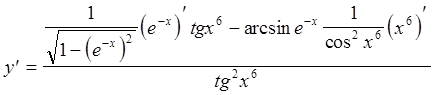 =
=
=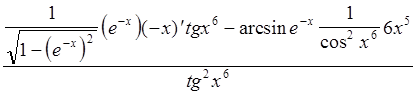 =
=
=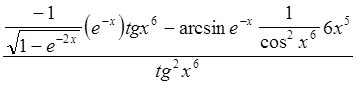 .
.
Задача. Найти ![]() , если
, если 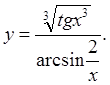 .
.
По формуле дифференцирования частного имеем:
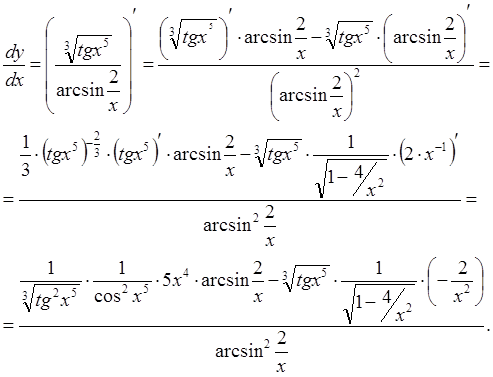
Приведем решение еще одного примера, все промежуточные выкладки в котором сделаны в уме.
Задача. Найти ![]() , если
, если 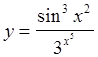 .
.
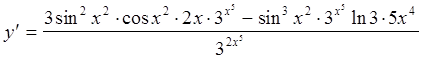 .
.
Задача 1г.
Для решения подобных задач используется метод логарифмического дифференцирования. Суть этого метода состоит в использовании равенства:
![]() .
.
Подобный прием применяется
для нахождения производных функций вида ![]() ,
а так же функций представляющих собой произведение большого числа множителей.
,
а так же функций представляющих собой произведение большого числа множителей.
Схему этого метода изложим сначала на примере.
Задача. Найти ![]() , если
, если
![]() (1)
(1)
Данная функция является сложной показательной функцией. Для ее дифференцирования используем логарифмическую производную. Опишем процесс нахождения производной сложной показательной функции.
Прологарифмируем равенство (1):
![]() Затем запишем правую часть
равенства в виде произведения, применив свойство логарифмической функции:
Затем запишем правую часть
равенства в виде произведения, применив свойство логарифмической функции:
![]() Продифференцируем получившееся
равенство:
Продифференцируем получившееся
равенство:
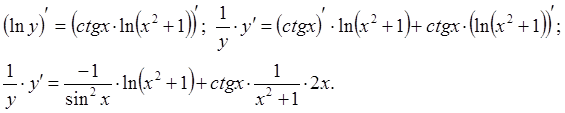
Выразим из последнего
равенства искомую производную ![]() :
:
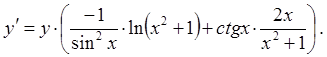 И, наконец, подставим вместо
функции
И, наконец, подставим вместо
функции ![]() ее выражение через
ее выражение через ![]() :
:
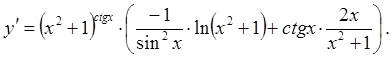
Задача. Найти ![]() , если
, если 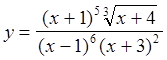 .
.
Прологарифмируем данное выражение:
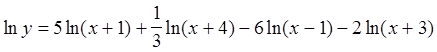 .
.
Возьмем производную от правой и левой части данного соотношения:
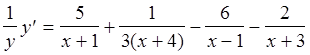 .
.
Тогда 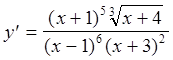 ×
×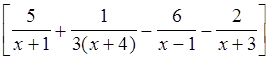 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.