Приближенные вычисления с помощью формулы Тейлора.
Сформулируем теорему Тейлора:
Функция ![]() ,
дифференцируемая
,
дифференцируемая ![]() раз в некотором
интервале, содержащем точку
раз в некотором
интервале, содержащем точку ![]() , может быть
представлена в виде суммы многочлена
, может быть
представлена в виде суммы многочлена ![]() -
ой степени и остаточного члена
-
ой степени и остаточного члена ![]() :
:
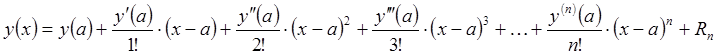 где
где 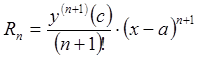 , где
, где ![]() --
некоторое число между
--
некоторое число между ![]() и
и ![]() .
.
Эта формула позволяет приближенно представить
(аппроксимировать) произвольную функцию ![]() в
виде многочлена и одновременно позволяет оценить погрешность
в
виде многочлена и одновременно позволяет оценить погрешность ![]() , которая во многих случаях может
быть сделана как угодно малой.
, которая во многих случаях может
быть сделана как угодно малой.
Частный, простейший случай формулы Тейлора при ![]() называется формулой Маклорена:
называется формулой Маклорена: 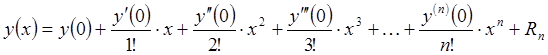 , где
, где
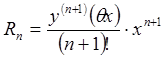 .
.
Запишем вид формулы Маклорена для функций ![]()
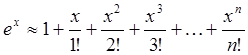
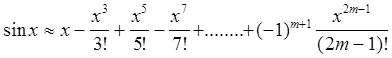
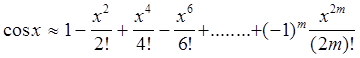
Отметим, что в формулах для ![]() значение
значение ![]() -- радианная мера угла.
-- радианная мера угла.
Приведем примеры вычисления приближенного значения приведенных функций с помощью формулы Тейлора.
Пример 1. Вычислить ![]() с точностью
с точностью ![]() .
.
Решение.
Выразим значение угла ![]() в радианах:
в радианах:
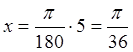
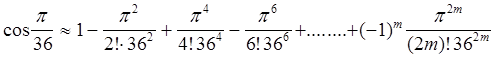
Оценим, сколько слагаемых необходимо взять для достижения заданной точности.
Погрешность данной приближенной формулы равна
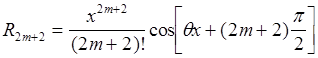 , где
, где ![]() . Избавимся от
неизвестной
. Избавимся от
неизвестной ![]() , используя неравенство
, используя неравенство ![]() , и для погрешности получим
неравенство:
, и для погрешности получим
неравенство:
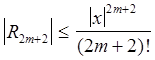 .
.
Чтобы определить, сколько слагаемых необходимо оставить, оценим значения остаточных членов:
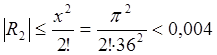
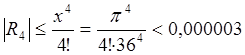
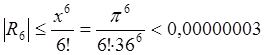
Величина ![]() , поэтому для
достижения заданной точности достаточно взять три первых слагаемых,
предшествующих
, поэтому для
достижения заданной точности достаточно взять три первых слагаемых,
предшествующих ![]() :
:
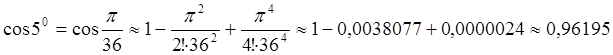
Ответ: ![]() .
.
Пример 2. Вычислить ![]() с точностью
с точностью ![]() .
.
Решение.
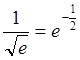 ,
,
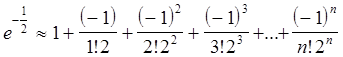
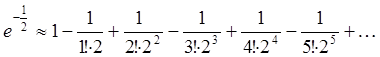
где 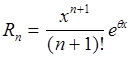 ,
, ![]() .
.
При 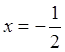 имеем
имеем ![]()
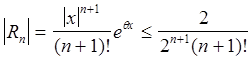 , так как
, так как ![]() .
.
Проверим, сколько слагаемых необходимо рассмотреть для достижения заданной точности.
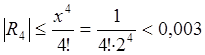
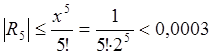
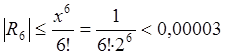
Величина ![]() , поэтому для
обеспечения требуемой точности возьмем первые пять членов разложения.
, поэтому для
обеспечения требуемой точности возьмем первые пять членов разложения.
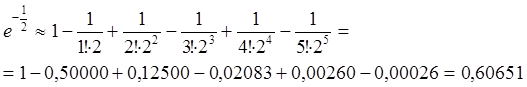 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.