


Методы решения некоторых задач, которые входят в экзаменационные билеты.
Правило Лопиталя.
Кроме способов, рассмотренных выше, весьма эффективным способом вычисления пределов является правило Лопиталя, которое использует понятие производной.
Сформулируем правило Лопиталя:
Предел отношения двух бесконечно малых или бесконечно больших величин равен пределу отношения их производных (если последний предел существует):
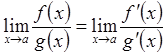 .
.
Правило Лопиталя можно применять в случае наличия
неопределенности ![]() и
и![]() .
.
Подчеркнем, что правило Лопиталя можно применять только к отношению двух функций и только при наличии неопределенности. Рассмотрим примеры.
1. 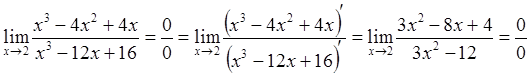
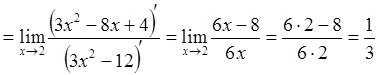
Рассмотренный пример иллюстрирует тот факт, что
правило Лопиталя допустимо применять несколько раз, если отношение производных
также представляет собой неопределенность вида ![]() или
или
![]() .
.
2. ![]()
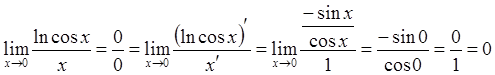 .
.
Приведенные выше пределы могут быть вычислены не только по правилу Лопиталя, но и путем элементарных преобразований. Рассмотрим примеры, решение которых существенно упрощается с использованием правила Лопиталя.
3. 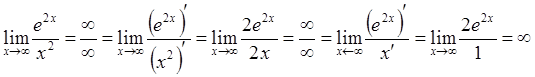 .
.
4. 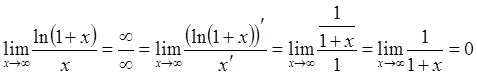 .
.
5. 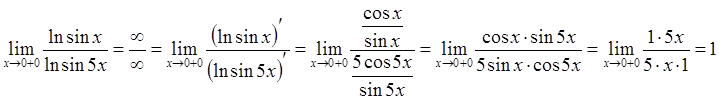
С помощью правила Лопиталя можно раскрывать
неопределенности вида ![]() и
и ![]() , предварительно записав ее как
частное
, предварительно записав ее как
частное ![]() или
или ![]() :
:
6. 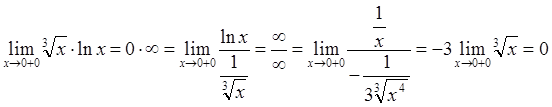 .
.
7. 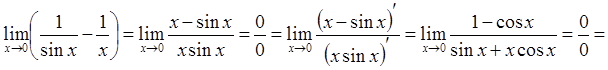
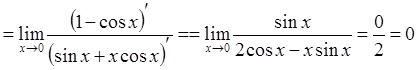
В некоторых примерах применение правила Лопиталя бессмысленно, так как предел отношения производных или не существует, или взятие производной не меняет принципиально функцию. В этих случаях предел можно попытаться вычислить с помощью элементарных преобразований:
8. 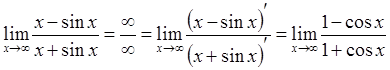 -- предел
отношения производных не существует, поскольку
-- предел
отношения производных не существует, поскольку ![]() не
существует. Тем не менее, исходный предел существует и вычисляется, если в
числителе и знаменателе дроби вынести за скобки множитель
не
существует. Тем не менее, исходный предел существует и вычисляется, если в
числителе и знаменателе дроби вынести за скобки множитель ![]() :
:
9. 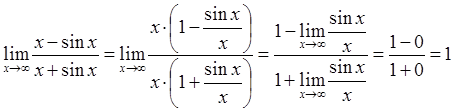 .
.
При вычислении предела 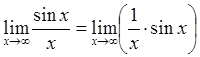 используется
теорема о том, что произведение бесконечно малой величины
используется
теорема о том, что произведение бесконечно малой величины ![]() на ограниченную
на ограниченную ![]() есть величина бесконечно малая.
есть величина бесконечно малая.
Правило Лопиталя используется также при раскрытии неопределенностей вида
![]() . При этом
предварительно необходимо применить основное логарифмическое тождество:
. При этом
предварительно необходимо применить основное логарифмическое тождество: ![]() , а затем неопределенность
, а затем неопределенность ![]() привести к виду
привести к виду
![]() или
или ![]() :
:
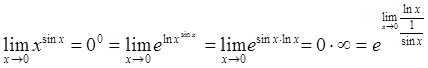 .
.
Тогда по правилу Лопиталя:
10. 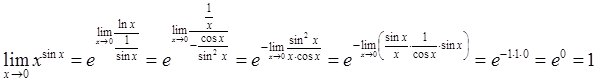
Рассмотрим пример, в котором возникает неопределенность ![]() .
.
11. ![]()
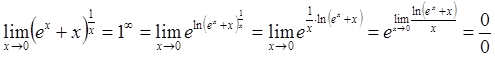
По правилу Лопиталя далее получим:
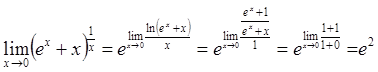
И, наконец, рассмотрим пример, где встречается неопределенность ![]() .
.
12. 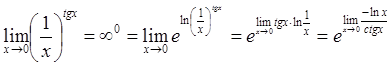 . Далее по правилу
Лопиталя имеем:
. Далее по правилу
Лопиталя имеем:
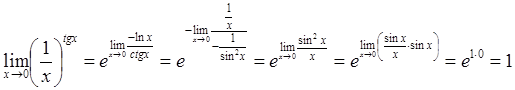 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.