Абстрактная и структурная теории конечных автоматов. Структура операционного устройства. Способы задания автоматов, страница 22

Представим функцию f  в виде (2):

 

Реализация функции f показана на рис. 3.8.

 

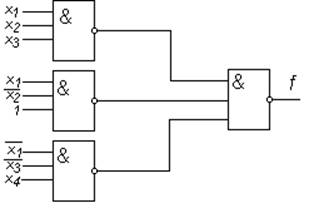
Рис.3.8

В случае, когда число элементарных произведений в выражении (2) больше m, то есть k > m, разделим все элементарные произведения на группы так, чтобы число элементарных произведений в каждой группе не превышало т.

Например, пусть задана функция

и требуется реализовать её на трёхвходовых элементах И-НЕ.

Представим функцию f  в виде

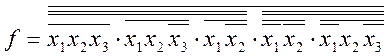
Ее реализация показана на рис. 3.9.

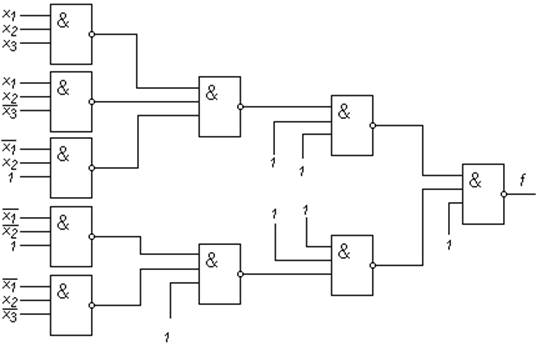
Рис.3.9

В случае, когда число сомножителей q в элементном произведении a_i (i=1,2,...,k) больше т, то есть q > m,  _i  можно представить в виде (4) путём разделения сомножителей на S групп. Причём число сомножителей в каждой группе должно быть меньше т.

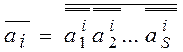                            (4), где  - элементарные произведения, число сомножителей в которых меньше т.

Реализация , представленного в виде (4), показана на рис. 3.10.

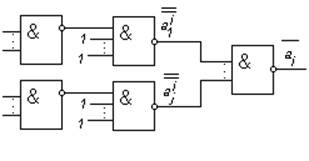
Рис.3.10

Например, задано элементарное произведение

Реализуем его с помощью трёхвходовых элементов И-НЕ. Представим a_i в виде (4):

Реализация  показана на рис. 3.11

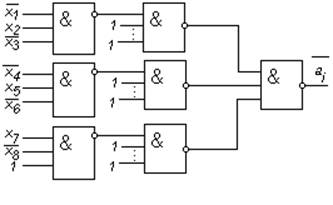
Рис.3.11

В общем случае, необходимо сначала разделить все произведения на группы, в каждой из которых число сомножителей не превышает m. Полученные группы снова разделить на группы, в каждой из которых число первоначальных групп не превышает m, и так продолжать до тех пор, пока число групп не будет меньше m. Каждая группа выделяется двумя отрицаниями.

Синтез логических схем состоит в следующем:

1. Ищется сокращенная дизъюнктивная нормальная форма синтезируемой функции.

2. Ищутся все приведенные системы импликант функции.

3. Из приведенных систем импликант выбирается минимальная.

4.  Найденная приведенная дизъюнктивная нормальная форма функции реализуется согласно рассмотренным выше примерам.

Пусть необходимо реализовать на двухвходовых элементах И-НЕ функцию   f=x₁ x _{2 3 4}   Vx _{12 34}   V ₁ x ₂ x ₃₄   V₁ x ₂ x ₃ x ₄   V

V ₁₂ x ₃ x ₄   V ₁₂ x _{3 4}  V ₁ x₂₃ x ₄   V ₁₂₃  x ₄  V ₁₂₃₄

Находим приведенные системы импликант и реализуем функцию

f  =x _{1 3 4}  V ₁ x ₃V _{1 2}  V₁x ₄   

Реализация показана на рис. 3.12

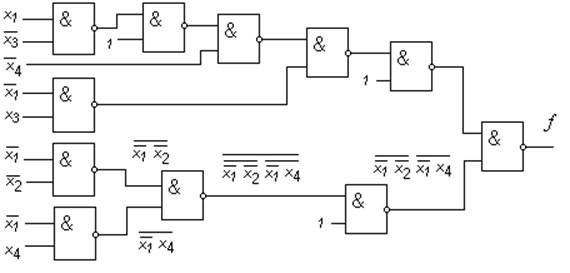
Рис.3.12

В случае необходимости синтеза нескольких функций, в ряде случаев, для минимизации аппаратурных затрат целесообразно просто реализуемые функции использовать в качестве переменной для синтеза более сложных функций.

Пусть необходимо построить функциональную схему для системы, заданной уравнениями  

y₁ = f₁ (x_1, x₂,…, x_n), 

y₂ = f ₂ (x_1, x₂,…, x_n) и более простая функция  y₁  уже построена.

Тогда новая функция  y^*₂ = f^*₂ (y_1, x_1, x₂,…, x_n) – не полностью определенная, и половина двоичных наборов являются неиспользуемыми. Это позволяет упростить функцию y^*₂= y₂ , для чего при нахождении сокращенной дизъюнктивной нормальной формы предполагаем, что минимизируемая функция на неопределенных наборах равна единице, а при отыскании приведенных систем простых импликант – нулю.

Подобным образом при минимизации функций переходов и выходов автомата учитываются прочерки в тех местах таблицы переходов и выходов, где соответствующие функции не определены, комбинации, неиспользуемые при кодировании состояний и входных сигналов автомата, необязательные функции возбуждения.

Например, функции возбуждения и выходов автомата Мура, построенного на логических элементах, реализующих функцию Шеффера (рис.3.15), заданного абстрактной таблицей переходов и выходов представленной на рис.3.13, и соответственно замененной после кодирования структурной таблицей (рис.3.14):

j₁ = t_{2 1}  V ₂ x₁= t_{2 1}      x₁

y₁ = t₁

j₂ = x₂  V t₁    = x₂  V t₁

y₂  = t₂

y = ₁t₂  = t₂

	w1	w2	w1
	а1	а2	а3
z1	а2	-	а1
z2	-	а3	а2
z3	а3	а1	-