Машинное (автоматное) изображение числа - это представление числа в разрядной сетке цифрового автомата. Обычно в цифровых автоматах рассматриваются либо область правильных дробей, либо область целых чисел со знаком и без знака. В первом случае положение запятой подразумевается после старшего разряда, во втором - после младшего. По степени сложности представления числа и управления разрядной сеткой форма с фиксированной запятой проще и обеспечивает более высокое быстродействие. Однако, диапазон представления чисел в такой форме достаточно узок. С точки зрения арифметических значений, в случае целых чисел:
1£½[A]ф.з½£ 2n-1, для правильных дробей:
2-n £½[A]ф.з½< 1- 2 - n, где [A]ф.з -машинное изображение числа A в форме с фиксированной запятой ; n-число разрядов разрядной сетки .
Изображение числа в форме с плавающей запятой определяется двумя параметрами: мантиссой mA и порядком PA, так что A = mA×qPA, где q - основание системы счисления. В этом случае диапазон обрабатываемых чисел значительно шире и зависит как от длины разрядной сетки, так и от используемой системы счисления:
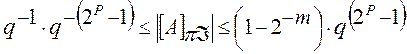, где p-число
разрядов, отводимых для представления порядка числа; m- число разрядов
для представления нормализованной мантиссы числа. Для представления чисел с
плавающей точкой применяются системы счисления с различными основаниями,
равными целой степени числа 2, при этом порядок часто представляется целым
числом, а мантисса – числом, в котором группы по r двоичных разрядов изображают цифры мантиссы с основанием
системы счисления q=2r. Использование для чисел с плавающей
запятой недвоичного основания несколько увеличивает погрешность (при заданном
числе разрядов мантиссы), но позволяет увеличить диапазон представления чисел и
уменьшить вероятность появления в ходе вычислений ненормализованных чисел.
Количество разрядов порядка и мантиссы числа рассчитываются исходя из
требуемого диапазона и относительной погрешности представления чисел. Допустим,
при заданной шестнадцатеричной системе счисления необходимо обеспечить диапазон
½A½£ 1010, погрешность 
.
Максимальное число, представляемое в разрядной сетке
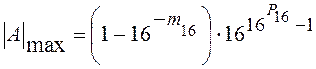, где m16
и P16 - число шестнадцатеричных
разрядов (m16 = 4 m2 ; P16 = 4 P2). Так как 1-16-m16 ≈ 1, а 
,
то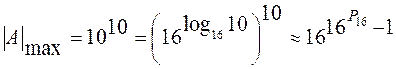 
; 
; 
;
; 
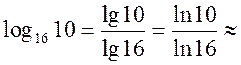
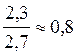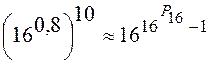
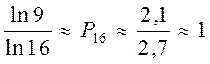
Один разряд шестнадцатеричной системы счисления равен четырём разрядам двоичной системы, следовательно, под порядок требуется четыре двоичных разряда.
Через относительную погрешность находим шестнадцатеричную мантиссу числа.
.
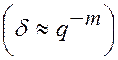Так как, 
, то 
; 
;
Следовательно, для обеспечения требуемой точности необходимо 5 разрядов шестнадцатеричной системы счисления, то есть 20 двоичных разрядов мантиссы.
Для выявления признака переполнения разрядной сетки используем модифицированные коды. Таким образом, общая длина разрядной сетки составит: N=2+P+2+m=28 разрядов. Для передачи информации обычно используются 8, 16, 32 или 64-х битные шины, так как основной единицей компьютерной информации является байт. Стандартизируем получившуюся разрядную сетку, дополнив её до 32-х разрядов. При этом увеличивается точность представления чисел, если часть разрядов будет добавлена к мантиссе числа. В случае увеличения числа разрядов порядка возрастёт диапазон обрабатываемых чисел.
Арифметические действия над числами с плавающей запятой требуют обработки по разным алгоритмам мантиссы и порядка числа. Для упрощения операций над порядком числа, его приводят к положительному значению, прибавляя смещение S=2K-1-1 , где k-число двоичных разрядов модуля порядка, то есть применяют для его представления смещенный код с отрицательным нулем. При этом, условие нормализации мантиссы числа имеет вид 2>½m½³1, а ее старший разряд, имеющий вес 1, в разрядной сетке предполагается по умолчанию.
3. СИНТЕЗ МИКРОПРОГРАММНЫХ АВТОМАТОВ
3.1 Способ получения абстрактных таблиц переходов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.