Абстрактная и структурная теории конечных автоматов. Структура операционного устройства. Способы задания автоматов, страница 21

 равна дизъюнкции всех существующих логических произведений, каждое из которых состоит из двух сомножителей: состояния и входного сигнала, образованных по следующему правилу:

Если в состоянии, обозначающем какой-либо столбец например r, таблицы переходов t_i  входит в прямом виде (t_i), а в состоянии, находящемся на пересечении с j строкой, обозначенной входным сигналом x_i, входит в инверсном виде (_i), то в качестве сомножителей логического произведения берутся состояния, обозначающие столбец r и входной сигнал, обозначающий j строку.

4. Выходная функция  y_i (i=1,2,…,p, где p-общее количество выходных каналов (микроопераций в автомате)) равна дизъюнкции всех существующих логических произведений, каждое из которых состоит из двух сомножителей: состояния и входного сигнала, образованных по следующему правилу:

Если на пересечении столбца r (r=1,2,…,k) со строкой j (j=1,2,…,l)  в таблице выходов автомата записан сигнал  y, то в качестве сомножителей логического произведения берутся состояния, отмечающие r-й столбец и входной сигнал, отмечающей j-ю строку.

В качестве примера найдем функции возбуждения и выходные функции для автомата, абстрактные таблицы переходов и выходов которого изображены на рис.3.2.

Таблица переходов .                Таблица выходов .

	t12	1 t2			t12	1 t2
	t12	---			y2 y3 y4	---
	1 t2	---			y2	---
	1 t2	---			y 1 y3	---
	---	t12			---	y 1 y4
	---	t12			---	y 1 y3
	---	t12			---	Ø

Рис.3.6

Закодируем состояния a₁ и a₂. Пусть a₁=10, a₂=01. Заменив в таблице (рис.3.2) абстрактные сигналы на структурные, получим таблицы, изображенные на рис.3.6.

Далее найдем функции возбуждения триггеров памяти ,  и выходные функции y_i.

j₁ ¹=₁ t₂x₁  V ₁t₂₁₃  V ₁ t₂₁ x₃

j₁ ⁰= t₁₂x₂₃   V  t_{1 2}

j₂ ¹= t₁₂x₂₃   V  t_{1 2}

j₂ ⁰= ₁ t₂x₁  V ₁t_{21 3}  V  ₁ t₂₁  x₃

y₁  = t₁₂₂   V  ₁t₂ x₁  V ₁t_{21 3} 

y₂  = t₁₂ x₁ x₂ x₃   V  t₁ x₂₃  

y₃  = t₁₂ x₁ x₂ x₃   V  t_{1 2}   V ₁t_{21 3} 

y₄  = t₁₂ x₁ x₂ x₃   V  ₁t₂ x₁

Управляющие автоматы с “жесткой логикой” обладают наибольшим быстродействием, однако, в отличие от управляющих устройств с программируемой логикой, изменить логику их работы можно только перепроектировав комбинационную схему.

3.5.  Синтез комбинационных схем в потенциальной

системе элементов

Пусть задана произвольная булева функция f = f (x_1, x₂,…, x_n).  Необходимо реализовать ее с помощью m входовых элементов, выполняющих логическую функцию g от m переменных (g=), то есть  найти функцию f  как суперпозицию функций g.

Пусть исходная булева функция f представлена в дизъюнктивной нормальной форме    f = a₁V a₂ V ... V a_k                          (1), где a_i (i=1,2,...,k) - некоторые элементарные произведения.

На основании правила де Моргана представим (1) в виде

 f = _{1 2} ...  _k                                                    (2)

Если k ≤ m и если каждое из элементарных произведений состоит менее, чем из m сомножителей, то выражение  (2) для функции f может быть переписано в следующем виде :

 f = g {g(a₁), g(a₂),..., g(a_k)}                                      (3)

То есть, реализация функции f, представленной в виде (3), может быть осуществлена, как показано на рис. 3.7.

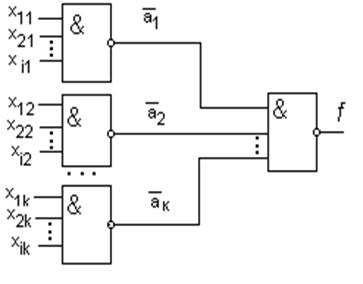
Рис.3.7

Например, пусть задана булева функция

и требуется реализовать её на трёхвходовых элементах И-НЕ.