






















УДК 519
МИНИСТЕРСТВО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
––––––––––––––
СЕРГИЕВ ПОСАДСКИЙ ФИЛИАЛ
МОСКОВСКОЙ ГОСУДАРСТВЕННОЙ АКАДЕМИИ
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
––––––––––––––––––––––
ЛОГИЧЕСКИЕ ФУНКЦИИ
ЭЛЕМЕНТЫ И СХЕМЫ
Лабораторная работа по курсу
«Дискретная математика»
 |
СЕРГИЕВ ПОСАД
2003
• Исследование логических функций, логических элементов и схем.
Логический преобразователь.
Генератор слов.
Вольтметр.
Логические пробники.
Источник напряжения + 5 В.
Источник сигнала "логической единицы".
Двухпозиционные переключатели.
Двухвходовые элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Микросхемы серии 74.
Переменные,
рассматриваемые в алгебре логики, могут принимать только два значения - 0 или
1. В алгебре логики определены отношение эквивалентности (обозначается знаком
=), операции сложения (дизъюнкции), обозначаемая знаком ![]() , умножения
(конъюнкции), обозначаемая знаками &,
, умножения
(конъюнкции), обозначаемая знаками &, ![]() или
точкой, и отрицания (или инверсии), обозначаемая надчеркиванием или апострофом
'.
или
точкой, и отрицания (или инверсии), обозначаемая надчеркиванием или апострофом
'.
Алгебра логики определяется следующей системой аксиом:
x = 1, если x
![]() 0; x = 0, если x
0; x = 0, если x ![]() 1;
1;
0&0 = 0; 1![]() 1 = 1
1 = 1
1&1 = 1; 0![]() 0 =0;
0 =0;
1&0 = 0&1
= 0; 0![]() 1 = 1
1 = 1![]() 0 = 1;
0 = 1;
![]() 1;
1; ![]() = 0.
= 0.
Запись логических выражений обычно осуществляют в конъюнктивной или дизъюнктивной нормальных формах. В дизъюнктивной форме логические выражения записываются как логическая сумма логических произведений, в конъюнктивной форме – как логическое произведение логических сумм. Порядок действий такой же, как и в обычных алгебраических выражениях. Логические выражения связывают значение логической функции со значениями логических переменных.
При преобразованиях логических выражений используются следующие логические законы и тождества
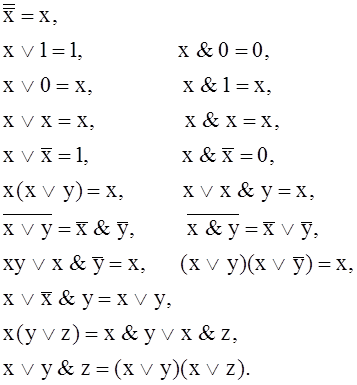
Любое логическое выражение, составленное из n переменных с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию n переменных. Такую функцию называют логической. В соответствии с аксиомами алгебры логики функция может принимать в зависимости от значения переменных значение 0 или 1. Функция n логических переменных может быть определена для 2n значений переменных, соответствующих всем возможным значениям n-разрядных двоичных чисел Основной интерес представляют следующие функции двух переменных х и у
f1(x,y) = x & y = x![]() y = x
y = x![]() – логическое
умножение (конъюнкция),
– логическое
умножение (конъюнкция),
f2(x,y) = x ![]() y – логическое сложение (дизъюнкция),
y – логическое сложение (дизъюнкция),
f3(x,y) = ![]() =
= ![]() – штрих Шеффера,
– штрих Шеффера,
f4(x,y) = ![]() =
= ![]() – стрелка Пирса,
– стрелка Пирса,
f5(x,y) = x![]() y =
y = ![]() – сложение по модулю 2,
– сложение по модулю 2,
f6(x,y) = ![]() –
равнозначность.
–
равнозначность.
Физическое устройство, реализующее одну из операций алгебры логики или простейшую логическую функцию, называется логическим элементом. Схема, составленная из конечного числа логических элементов по определенным правилам, называется логической схемой. Основным логическим функциям соответствуют выполняющие их схемные элементы.
Так как область определения любой функции n переменных конечна (2n значений), такая функция может быть задана таблицей значений f(i), которые она принимает в точках i, где i= 0,…,2n—1. Такие таблицы называют таблицами истинности. В таблице 1 представлены таблицы истинности, задающие указанные выше функции.
Таблица 1
|
№ |
Значения переменных |
Функции |
||||||
|
x |
у |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
2 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
3 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
Если число логических переменных не превышает 5-6, преобразования логических уравнений удобно производить с помощью карт Карно. Цель преобразований - получение компактного логического выражения (минимизация). Минимизацию производят объединением соседних наборов (термов). Объединяемые наборы должны иметь одинаковые значения функции (все 0 или все 1). Для наглядности рассмотрим пример: пусть требуется найти логическое выражение для мажоритарной функции fm трех переменных x, у, z, описываемой таблицей истинности, показанной в Таблице 2.
Таблица 2
Мажоритарная функция
|
№ |
x |
y |
z |
fm |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
Здесь номер строки равен числу i= 22x+21y+20z, образованному значениями переменных.
Составим карту Карно. Она представляет собой нечто похожее на таблицу, в которой наименования столбцов и строк представляют собой значения переменных, причем переменные располагаются в таком порядке, чтобы при переходе к соседнему столбцу или строке изменялось значение только одной переменной. Например, в строке xy таблицы 3 значения переменных xy могут быть представлены следующими последовательностями 00,01,11,10 или 00,10,11,01. Таблицу заполняют значениями функции, соответствующими комбинациям значений переменных. Полученная таким образом таблица выглядит, как показано ниже (таблица 3).
Таблица 3
Карта Карно
мажоритарной функции
|
xy |
00 |
01 |
11 |
10 |
|
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
yz xy xz
На карте Карно отмечаем группы, состоящие из 2k соседних ячеек (2,4,8, ) и содержащие 1, так как они описываются простыми логическими выражениями. Три овала в таблице определяют логические выражения xy, xz, yz. Каждый овал, объединяющий две ячейки, соответствует логическим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.