Лекция 8
Построение эпюр внутренних усилий в статически неопределимых системах
8.1. Определение внутренних силовых факторов
При вычислении внутренних силовых факторов (изгибающих моментов М, поперечных и продольных сил Qи N) найденные значения неизвестных следует рассматривать как внешние силы, приложенные к основной системе.
Вначале рассмотрим метод определения изгибающих моментов. От единичных значений неизвестных моменты равны Мх, М2, ..., Мn. Для получения моментов от истинных значений неизвестных необходимо моменты М умножать на значения неизвестных X, тогда получим «исправленные» моменты от лишних неизвестных M1X1, M2X2, М3Х3. Сложив эти значения и прибавив к полученному результату моменты МPв основной системе, получим для произвольного сечения в какой-либо точке k момент в заданной системе
Мк = Mk1 X1 + Мк2Х2 + ... + MknXn + М°кP.
Аналогичные формулы можно написать для поперечных и продольных сил
Ок = Qk1 X1 + Qk2 X2 г + … + Qkn Xn + QkP; Nk = Nk1 X1 + Nk2X2 + ... + Nkn„Xn + NiP.
Для построения окончательной эпюры моментов необходимо построить «исправленные» эпюры М1Х1 ,М2Х2, ..., МпХп. Для этого все ординаты единичных эпюр следует умножить на соответствующие значения неизвестных и составить окончательную эпюру моментов путем простого суммирования исправленных эпюр и эпюры от нагрузки Мр.
Для построения эпюр Q и N в заданной статически неопределимой системе нет необходимости пользоваться формулами (6.12), а проще построить их на основании окончательной эпюры моментов.
Рассмотрим технику решения задач на примере, для которого проведен расчет в прошлой лекции.
Пользуясь найденными значениями неизвестных X1 = - 5,92562 кН, Х2 = 0,31818 кН, Х3 == - 0,02479 кН/м и умножив на них ординаты единичных эпюр, изображенных на рис. 6.6,б, в, г, получим исправленные эпюры, изображенные на рис. 6.7, а, б, е. Сложив эти эпюры и прибавив к ним эпюру от нагрузки, показанную на рис. 6.6, а, получим окончательную эпюру моментов в заданной системе (рис. 6.8, а).
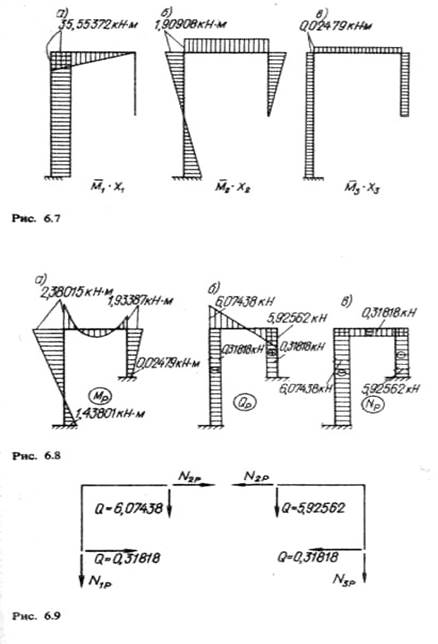
Для построения эпюры Qвоспользуемся известным дифференциальным соотношением dM/dx = Q.
Для стержней, в пределах которых эпюра Мочерчена прямой линией, производная dM/dx определится как угол наклона прямой линии к оси стержня dM/dx= ±tga.
Условимся ординаты эпюры моментов откладывать со стороны растянутых волокон. Для определения знака поперечной силы будем поворачивать ось стержня до совмещения с линией эпюры моментов так, чтобы осуществить это кратчайшим путем. Если поворот происходит по ходу часовой стрелки, то поперечная сила будет положительной (Q > 0). При движении против хода часовой стрелки Q < 0. Некоторое затруднение возникает, если эпюра М на какомлибо стержне криволинейная, тогда необходимо рассмотреть такой стержень как балку на двух опорах, приложив к нему нагрузку и концевые моменты, и построить для него эпюру Q.
Для построения эпюры Nпроще всего воспользоваться методом вырезания узлов, при этом найденные значения Q необходимо приложить к соответствующим сечениям как внешние силы. Составив сумму проекций найденных сил Q и неизвестных N, легко определить значения последних.
Продолжим пример, для которого построена эпюра моментов. Для левой стойки имеем
Qp = - (2,38015 + 1,43801)/12 = = - 0,31818 кН.
Для правой стойки
Qp = (1,93387 - 0,02479)/6 = + 0,31818 кН.
Для горизонтального стержня эпюру Q построим как для простой балки с равномерной нагрузкой q = 2 кН/м и моментами на концах 2,38015 кНм и 1,93387 кНм.
Окончательная эпюра Qp показана на рис. 6.8, б.
Для определения значений продольных сил последовательно вырежем левый и правый (верхние) узлы рамы (рис. 6.9). Из условия равновесия находим
N1p = - 6,07438 кН,
N2p = - 0,31818 кН,
N3p = = - 5,92562 кН.
Окончательная эпюра Npв статически неопределимой раме показана на рис. 6.8, в.
8.2. Проверка правильности решения
В процессе расчета статически неопределимой рамы обычно проводятся проверки промежуточных вычислений, а также проверка окончательных результатов. В первую очередь желательно проверить правильность вычислений коэффициентов канонических уравнений. Для этой цели строится эпюра MS, являющаяся суммой всех эпюр от единичных pначений лишних неизвестных MS = M1 + M2 + ... + Мп.
Вычислив интеграл Мора, получим сумму коэффициентов при неизвестных в k-ом каноническом уравнении
![]()
![]()
![]()
![]()
![]() dks = Mk Msds = Mk (M1 +
M2 + +
Mn )ds =
EI EI = Mk M1ds + Mk M2ds + + Mk Mnds
dks = Mk Msds = Mk (M1 +
M2 + +
Mn )ds =
EI EI = Mk M1ds + Mk M2ds + + Mk Mnds
n
=dk1+dk2 dkn = dki
i=1
Принимая k = 1, 2,..., n, можем проверить все коэффициенты канонических уравнений. Суммы элементов первой, второй и т.д. строк, соответственно, равны результатам перемножения каждой из единичных эпюр с эпюрой Ms.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.