Оценивание параметров уравнений двухшаговым методом наименьших квадратов

Оценивание параметров уравнений двухшаговым методом наименьших квадратов (2МНК)

Двухшаговый метод наименьших квадратов используется в том случае, когда система уравнений сверхидентифицируемая, т.е. невозможно однозначно оценить коэффициенты структурной формы на основании полученных коэффициентов приведенной формы модели.

Суть двухшагового метода заключается в следующем:

1) На основании приведенной формы рассчитывают параметры уравнений приведенной формы, затем подставляют значения факторных (экзогенных) переменных и вычисляют теоретические значения эндогенных переменных.

2) Если в структурной модели есть точно идентифицируемые уравнения, то коэффициенты регрессии находятся для них косвенным методом наименьших квадратов из системы приведенных уравнений.

Для остальных сверхидентифицируемых уравнений (когда ) следует подставить теоретические значения эндогенных переменных вместо фактических в структурную форму модели и применить классический метод наименьших квадратов.

Пример. Имеются следующие данные по группе предприятий:

где  -экспорт, млн. ден. един.

 - импорт, млн. ден. един.;

 - доля сертифицированной продукции в валовом выпуске, %;

 - инвестиции, млн. ден. един.;

 - коэффициент обновления основных фондов, %.

Система современных экономических уравнений для заданного набора переменных может быть записана в следующем виде.

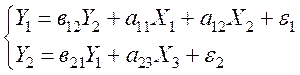         структурная форма                  (12.11)

Проверим каждое уравнение системы на идентифицируемость.

В первом уравнении присутствуют две эндогенные переменные  и  (Н=2) и отсутствует одна экзогенная переменная  (D=1). Следовательно, первое уравнение идентифицируемое (D+1=Н).

Во втором уравнении присутствуют две эндогенные переменные ( и ) и отсутствуют две экзогенные переменные  и . Так как Д+1≥Н, второе уравнение сверхидентифицируемое.

Система уравнений (12.11) в целом является сверхидентифицируемой. Для оценки параметров сверхидентифицируемого второго уравнения применим двухшаговый метод наименьших квадратов.

Решение:

1. Построим приведенную форму модели и рассчитаем её коэффициенты:

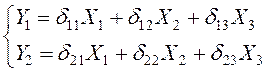                                                                (12.12)

По методу наименьших квадратов определяем коэффициенты приведённой формы. Для нахождения коэффициентов первого уравнения d₁₁, d₁₂ d₁₃  необходимо решить следующую систему:

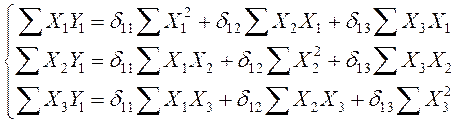                                (12.12)

Представим результаты расчетов в следующей таблице:

Подставив полученные итоговые значения в выражение (12.12) получим:

;  ;  .

Первое уравнение приведённой формы будет иметь вид:

Аналогичные расчеты выполним для второго уравнения

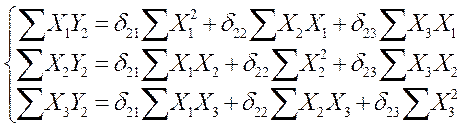                               (12.13)

Из выражения (12.13) получаем следующие значения параметров:

                    .

Приведенная форма модели имеет вид:

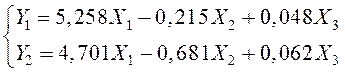                                                 (12.14)

Чтобы построить первое уравнение структурной формы, выразим переменную  X₃ из второго уравнения приведенной формы и подставим в первое уравнение (12.11):

.

На основании первого уравнения приведённой формы вычислим теоретические значения эндогенной переменной ,  подставим эти значения вместо исходных значений переменной  и рассчитаем коэффициенты второго сверхидентифицируемого уравнение структурной формы.

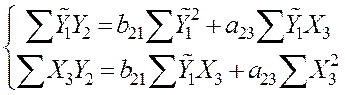                                         (12.15)

Второе уравнение структурной формы модели имеет вид:

Тогда структурная форма будет иметь вид:

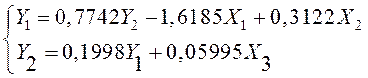                                               (12.16)

Если бы для каждого уравнения структурной формы (12.11) отдельно вычислить параметры при помощи  метода наименьших квадратов, полученные результаты отличались бы от тех, которые получены косвенным или двухшаговым методом наименьших квадратов. Причины такого расхождения пояснены в работах [  ].