Исследование методов оптимизации второго порядка на задачах экономики

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УО «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра прикладной математики и экономической кибернетики

КУРСОВОЙ ПРОЕКТ

Пи дисциплине: Численные методы

На тему: Исследование методов оптимизации второго порядка на задачах экономики (Метод Ньютона, Метод Ньютона - Рафсона)

Студент

ФМ, 2-ой курс, ДКК                                                      

Руководитель

Доцент                                                                                 

Минск, 2015

РЕФЕРАТ

Курсовая работа: 31 с., 6 рис., 3 табл., 19 источников

МЕТОДЫ ОПТИМИЗАЦИИ ВТОРОГО ПОРЯДКА, МЕТОД НЬЮТОНА, МОДИФИКАЦИИ МЕТОДА НЬЮТОНА.

Объект исследования  — методы оптимизации второго порядка на задачах экономики.

Предмет исследования  — метод Ньютона для решения систем нелинейных уравнений и его модификации.

Цель работы: продемонстрировать эффективность использования метода Ньютона и метода Ньютона – Рафсона для решения систем нелинейных уравнений.

Методы исследования: описания, классификации, аналитические, математические. 

Исследования и разработки: изучены подходы к получению расчетных формул для метода Ньютона, алгоритмы нахождения корней системы нелинейных уравнений для разных случаев, проанализирована эффективность применения данных методов на практике.

Практическая значимость: Исследование помогает сделать вывод о рациональности использования метода Ньютона и его модификаций для решений прикладных экономических задач, в частности, задачи нахождения оптимального сочетания факторов производства.

Автор работы подтверждает, что приведенный в ней расчётно-аналитический материал правильно н объективно отражает состояние исследуемого процесса, а все заимствованные из литературных и других источников теоретические, методологические и методические положения и концепции  сопровождаются ссылками на их авторов.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.. 4

1. Теоретические основы метода Ньютона. 5

1.1 Различные подходы к получению расчётных формул. 5

1.2 Основная теорема о сходимости метода Ньютона. 7

1.3 Критерий окончания итерационного процесса. 9

2. Метод Ньютона для решения систем нелинейных уравнений. 11

2.1. Описание метода. 11

2.2. Сходимость метода. 13

2.3. Трудности использования. 14

3. Обзор модификаций метода Ньютона. 15

3.1 Проблемы, связанные с использованием метода Ньютона. 15

3.2 Модификации метода Ньютона. 16

4. Применение метода Ньютона и Ньютона – Рафсона в экономике. 21

ЗАКЛЮЧЕНИЕ.. 30

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 31

ВВЕДЕНИЕ

На практике в расчетно-экономической деятельности задача нахождения экстремума функции встречается довольно часто. Как будет показано ниже, эта задача может быть переквалифицирована в задачу решения системы нелинейных уравнений. Посему целесообразно использовать метод Ньютона для решения подобных проблем. В частности в данной работе будет рассмотрена задача нахождения оптимального сочетания факторов производства как частный случай задач оптимизации.

Объектом исследования являются методы оптимизации второго порядка на задачах экономики.

Предмет исследования составляют метод Ньютона для решения систем нелинейных уравнений и его модификации. Так как целью работы является продемонстрировать эффективность использования метода Ньютона и метода Ньютона – Рафсона для решения систем нелинейных уравнений, целесообразно достичь ее посредством выполнения ряда задач. Во-первых необходимо рассмотреть теоретические основы метода Ньютона для решения нелинейных уравнений. Во-вторых необходимо определить алгоритм решения систем нелинейных уравнений методом Ньютона. В-третьих, рассмотреть ряд модификаций метода Ньютона, изучить в каких случаях они могут быть полезны.  В-четвертых, продемонстрировать, насколько данный алгоритм может быть применен на практике. Для достижения поставленных задач используются различные методы исследования: описания, классификации, аналитические и математические методы. 

Наконец, структура работы представлена:

§  Главой 1. Теоретические основы метода Ньютона

§  Главой 2. Метод Ньютона для решения систем нелинейных уравнений

§  Главой 3.  Обзор модификаций метода Ньютона

§  Главой 4. Применение метода Ньютона и Ньютона – Рафсона в экономике

1. Теоретические основы метода Ньютона

1.1 Различные подходы к получению расчётных формул.

Покажем, как поиск корня системы нелинейных уравнений можно свести к задаче минимизации функции и наоборот, задачу о минимизацию к решению систем уравнений[1].

Предположим, что в области D пространства необходимо решить систему уравнений 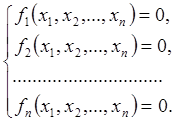(1.1).

                                      (1.1)

Пусть известно, что в D существует решение системы (1.1). Определим целевую функцию Ф(х) формулой

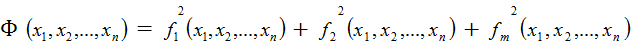          (1.2)

В области D целевая функция Ф(х) > 0. Минимальное значение функция Ф(х) достигает на векторе  который обращает все  в нуль. Поэтому решение системы (1.1) эквивалентно поиску минимума Ф, определенной формулой (1.2), т.е. найти .

Если минимальное значение Ф(х) в области D строго больше нуля, то система уравнений (1.1) не имеет решений.

При условии, что все функции ) непрерывно дифференцируемы в открытой