Модель скользящего среднего первого порядка. Независимые нормально распределенные случайные величины

Модель скользящего среднего первого порядка MA(1)

                                                      (1)

где  независимые нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией :

,    ,   .                                               (2)

В силу (1), (2):

,                                                    (3)

                              (4)

Найдем ковариацию .

В силу (1):

                                     (5)

В силу (1), (2), (5):

Итак,

                                             (6)

Найдем ковариацию , где .

В силу (1):

                                             (7)

В силу (1), (2), (7)

                                    (8)

В силу равенств (3), (4), (6), (8) процесс MA(1) является стационарным в слабом смысле (при любых значениях коэффициентов  и .

В силу (4), (6):

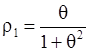                                         (9)

Из равенства (9) следует, что

                                            (10)

причем  при ,  при .

Из (9):

                                (11)

Отсюда:

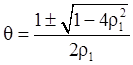                                (12)

Несложно показать, что при :

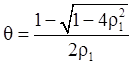                                (13)

Оценивание параметров

В силу (3) в качестве оценки  параметра  можно взять :

                         (14)

В силу (13), считая, что , оценку  параметра  можно находить по формуле:

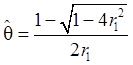,                                           (15)

где  – выборочный коэффициент ковариации между  и .

Найдем формулу для оценки параметра .

Из (4):

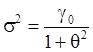                             (16)

Слдедовательно, оценку  параметра  можно искать по формуле:

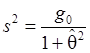                             (17)

где  выборочная дисперсия .

Прогнозирование

Прогнозирование на один период вперед.

В силу (1):

                           (18)

Отсюда:

                (19)

Найдем формулу для .

В силу (1):

                                                      (20)

Следовательно:

                    (21)

В частности:

                                    (22)

Следовательно, зная , с помощью формулы (21) можно рекуррентным образом найти  , в том числе .

В силу формул (19), (21), (22) прогнозное значение  можно искать по формуле:

,                                                           (23)

где значение  находится рекуррентным образом с помощью формул:

                                                            (24)

                                        (25)

Прогнозирование на несколько периодов вперед

В силу спецификации модели (1):

                                (26)

Следовательно,

                                  (27)

В силу (27) в качестве прогнозного значения   при  естественно взять :

,                               (27’)

Модель скользящего среднего порядка   MA(q)

Спецификация модели:

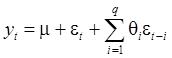                                                (28)

где  независимые нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией :

,    ,   .                                               (29)

В силу (28):

                                                     (30)

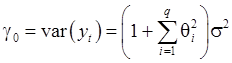                        (31)

Найдем ковариацию

В силу (28):

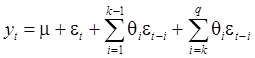        при                    (32)

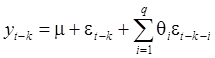                            (33)

Следовательно, при   в силу (29):

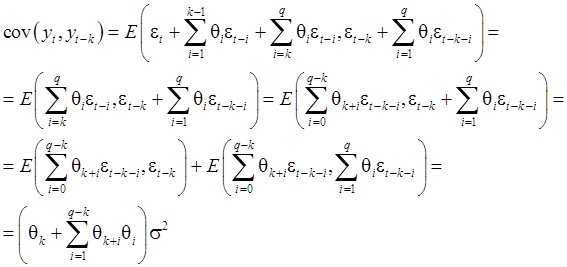
Итак,

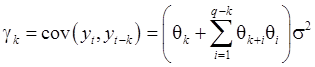
                                           (34)

Из (28), (33), (29) вытекает, что

                                                           (35)

В силу равенств (30), (31), (34), (35) процесс MA(q) является стационарным в слабом смысле (при любых значениях коэффициентов  и ).

В силу (31), (34), (35):

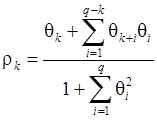
                                                   (36)

                                                                       (37)

Соотношения (36), (37) служат основой для определения порядка  модели скользящего среднего MA(q).

Порядок  модели скользящего  равен значению  при котором  и   при .

Оценивание параметров

В силу (30) в качестве оценки  параметра  можно взять :

                         (38)

В силу равенств (36) оценки  параметров , ,  можно находить с помощью следующей системы (нелинейных) уравнений:

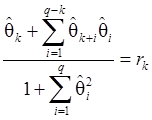,                           (39)

где  – выборочный коэффициент ковариации между  и .

В силу 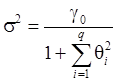(31):

                        (31)

Следовательно, оценку  параметра  можно находить по формуле:

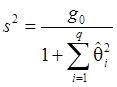,                                  (32)

где  выборочная дисперсия .

Прогнозирование

В силу спецификации модели (28):

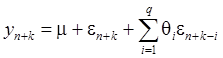                                      (33)

Следовательно, при :

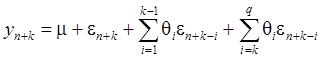                              (34)

В силу (34):

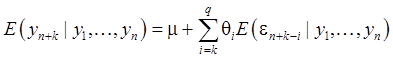                (35)

Эту формулу можно записать также в виде:

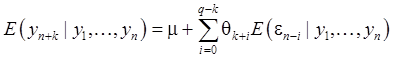                (36)

Найдем формулы для .

В силу (28):

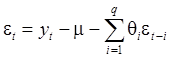                                                (37)

Следовательно,

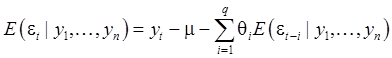                (38)

В частности:

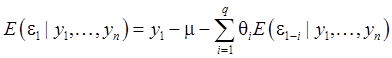                (39)

Следовательно, зная , , с помощью формулы (38) можно рекуррентным образом найти  .

В силу формул (36), (39), (38) прогнозное значение  можно искать по формуле:

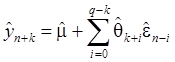,                                               (40)

где значения  находится рекуррентным образом с помощью формул:

,

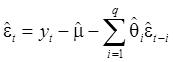,                                 (41)

Из (33) следует, что при

                                              (42)

Следовательно, при  в качестве прогнозного значения  естественно взять :

,                                                       (43)

Модель авторегрессии – скользящего среднего порядка   ARMA(p,q)

Спецификация модели:

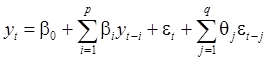                                                    (1)

где  независимые нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией :

,    ,   .                                               (2)

Будем считать, что случайный процесс  является стационарным (в слабом смысле), т.е.

,   ,                            (3)

В силу (1)-(3):

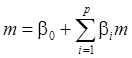                                            (4)

Отсюда:

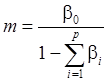                                     (5)

В силу (1)-(3):

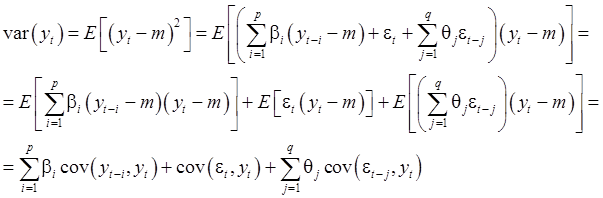
Итак,

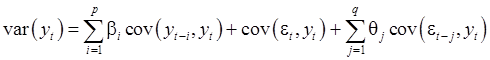                                (6)

В силу (1):

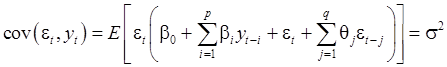                                        (7)

В силу (1) при  :

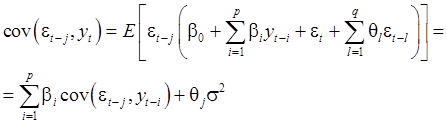                                        (8)

Подставим (7), (8) в (6):

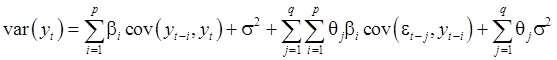                  (9)

Прогнозирование

В силу спецификации модели (1):

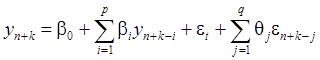                   (10)

Следовательно,

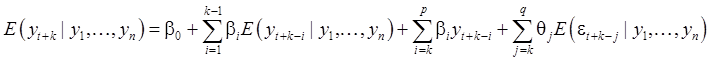           (11)

В силу (11):

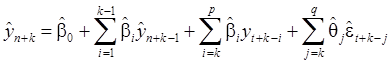                            (12)

Прогнозные значения  находятся следующим образом.

В силу (1):

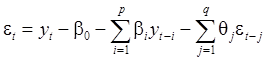                             (13)

Следовательно,

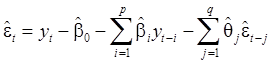   при                      (14)

Считая, что

                                                (15)

по формуле (14) рекуррентным образом начиная с  можно найти  для всех .

После нахождения , , формулу (12) можно рекуррентным образом (начиная с ) использовать для нахождения прогнозных значений .

Модель авторегрессии – проинтегрированного скользящего среднего порядка   ARIMA(p,q,r)

Обозначим:

                                                (1)

                                          (2)

                                 (3)

Случайная последовательность  называется рядом ARIMA(p,q,r), если ряд  является (стационарным) рядом ARMA(p,q), т.е. ряд  является стационарным (в слабом смысле) и имеет место равенство:

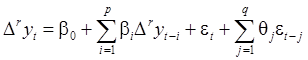                                                        (4)

где  независимые нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией :

,    ,   .                                               (5)

Оценивание параметров для модели ARIMA(p,q,r) сводится к оценке параметров модели ARMA(p,q) для ряда , 

Прогнозирование осуществляется в два этапа.

На первом этапе находятся прогнозные значения   ряда  в рамках модели