Дифференцирование степенных рядов. Исследование сходимости ряда

Пример 1

∞                     1

n−1

Дан сходящийся ряд ∑ (−1⁾    ₂ . Оценить ошибку,

n=1                  n

допускаемую при замене суммы этого ряда: 

1)  суммой первых трех его членов 

2) 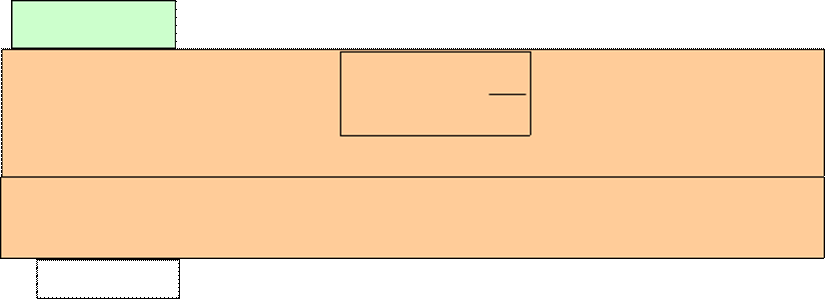 суммой первых его четырех членов      Решение.

1) Из формулы S = S_n + r_n находим S = S₃ + r₃ .  Или

| rn |< an+1

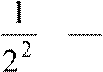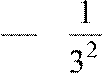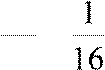
S = 1−  +  + r₃. Откуда   S =  + r₃. По теореме Лейбница . Значит | r₃ |< a₄ или | r₃ |<  = .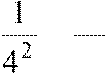

Так как r₃ = −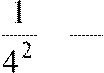 +  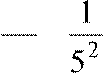−.....+, то   r₃ < 0 

(см.  т. Лейбница)  Для ряда вида  − a1 + a2 − a3 +...+ (−1)n an +...,  an > 0оценка суммы ряда имеет вид − a1 < S < 0 .
Тогда  или сумма	S	с избытком.

2) Аналогично S = S₄ + r₄. Или S .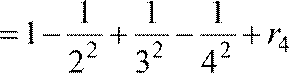

Откуда S =  + r₄. Далее| r₄ |< a₅ или | r.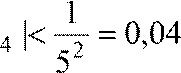

Так как r₄ = + −.....+, то   r₄ > 0. Значит, сумма ряда

115 S ≈ 144

с недостатком

Пример 2

∞             ⁿ⁻¹ 1

Проверить, что  ряд ∑ (−1)             сходится. 

n=1                      n

Сколько нужно взять членов ряда, чтобы вычислить его сумму с точностью до 0,01 ? 

Решение.

1) Ряд сходится, так как все условия т. Лейбница  выполнены.

| rn |< an+1

2) Так как S = S_n + r_n и верна оценка , то 

1

требуемое n найдем из условия: a_n+1 =< 0,01. n +1

1

Из уравнения = 0,01 находим n = 9999  n +1

Итак, | r₉₉₉₉ |< 0,01 причем 0 < r₉₉₉₉ < 0,01. Значит

S = S₉₉₉₉ + r₉₉₉₉ или    S ≈ S₉₉₉₉ с  недостатком.

Пример 3Сколько нужно взять членов ряда

∞              ⁿ⁻¹           n

∑ (−1)  _n , чтобы вычислить его сумму с n=1 (2n +1)5 точностью до 0,01 ?

1) Ряд сходится по  т. Лейбница 2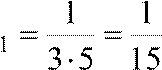) a, a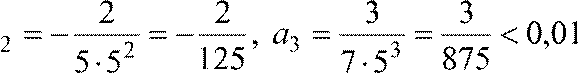. Значит, надо взять        два        члена        ряда         S = S₂ + r₂,                  или 

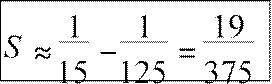, (с недостатком, так r₂ > 0)

Пример 4   Найти сумму ряда

1+ 2x +3x² + 4x³ +...+...(| x |<1)

Применим  дифференцирование степенных рядов.

Рассмотрим геометрическую прогрессию

1+ x + x² + x³ +...+... = ¹   при (| x |<1)

1− x Дифференцируем этот ряд

(1+ x + x² + x³ +...+...)′ = ( ¹                                        ′

Применим  интегрирование степенных рядов.

Рассмотрим геометрическую прогрессию

1+ x + x² + x³ +...+... = ¹   при (| x |<1)

1− x

Интегрируем этот ряд

x                     ^{2         3}                               x        1

∫(1+ x + x + x +...+...)dx = ∫   dx. 

0                                                                  ₀ 1− x

Отсюда

x ), 

Ряд сходится при −1 ≤ x < 1   !

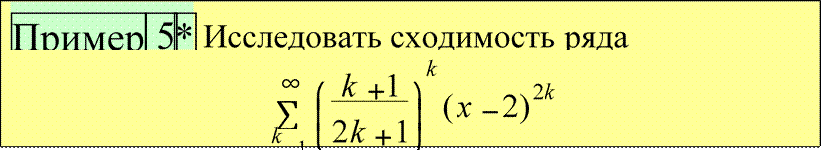
k ⎛ k +1 ⎞ Здесь an = 0 при n = 2k −1 и an = ⎜ ⎟ при n = 2k ⎝2k +1⎠

Находим 

1                         1                            ⎛2k +1⎞

R = =    = lim      ⎜      ⎟      =    2 nlim→∞ n | an |     lim 2k ⎛⎜ k +1 ⎟⎞k    k→∞ ⎝ k +1 ⎠ k→∞   ⎝2k +1⎠

При x − 2 =   2 имеем числовой ряд

k

⎛         ⎞

^∞ ⎛ k +1 ⎞k                         ⎜ k +1 ⎟       ∞ ⎛         1     ⎞k

∞

∑ ⎜ ⎟ 2_k = ∑ ⎜ ⎟ = ∑ ⎜1+ ⎟ k₌₁ ⎝2k +1⎠ k=1 ⎜_{⎜k +} 1 ⎟_⎟ k=1 ⎝ 2k +1⎠

⎝      2 ⎠

k

⎛        1    ⎞            ⎛         1    ⎞

lim⎜1+           ⎟   = lim⎜1+                  ⎟=         e ≠ 0

k→∞⎝      2k +1⎠      k→∞⎝     2k +1⎠

то ряд расходится, ибо общий член ряда не стремится к нулю.

Аналогично, при x − 2 = − 2 ряд расходится.

Итак,

2−

2 < x < 2+

2

— область сходимости ряда

Среди различных аналитических аппаратов исследования функций первое место по своей простоте и удобству употребления занимают  степенные ряды. Идея проста: функция, которую мы хотим изучить, представляется как предел частичных сумм  простейших степенных функций.

Пусть задана f (x)   в окрестности точки  x = x₀ .

Предположим,  что f (x) разлагается в  ряд по степеням

(x − x₀ ): т.е. ряд имеет вид f (x) = a₀ + a₁(x − x₀ ) + a₂ (x − x₀ ⁾² +..+ a_n (x − x₀ ⁾ⁿ +...(1) с радиусом сходимости R,    (| x − x₀ |< R)

Этот ряд на интервале сходимости   | x − x₀ |< R   можно  дифференцировать бесконечно число раз:

f ′(x) = a₁ + 2⋅a₂ ⋅(x − x₀ )+3⋅a₃ ⋅(x − x₀ ⁾²..+ n⋅a_n ⋅(x − x₀ ⁾ⁿ⁻¹...

f ′′(x) = 2⋅1⋅a₂ +3⋅2⋅a₃(x − x₀ ) +..+ n⋅(n −1)⋅a_n ⋅(x − x₀ ⁾ⁿ⁻²...

……………………………………………………………… ^{f (n)}(x) = n⋅(n −1)⋅...⋅1⋅a_n + (n +1)⋅n⋅...⋅3⋅2a_n+1 ⋅(x − x₀) +...

Положим в каждом равенстве x = x₀. Тогда последовательно получаем коэффициенты Тейлора:

f ′(x0 ), a = f ′′(x0 ),…a = f (n) (x0 ) a₀ = f (x₀ )     a1 = 2 n ,.

1!                    2!                     n!

Итак, если функция f (x) разлагается в  ряд по степеням

(x − x₀ ), то этот ряд имеет  вид      

f ′′(x ) f (x) = f (x0 )+ f ′(x0 )(x − x0 ) + (x − x0 )2 +...
f (n) (x )                            ∞        (n)                           n +    0 (x − x0 )n +... = ∑ f   (x0)(x − x0)           n!    n=0   n!	(2)

	Определение.	Степенной ряд вида (2) называется рядом функции f (x) в точке x0. Если x0 = 0, то ряд  f n (0)   n                ∞    f (n)(0)    n f ′(0)x +..+    x +...= ∑ x (3) n!  n=0   n! рядом Маклорена.
	Тейлора  f (x) = f (0) + называется

Теперь откажемся от этого предположения. Будем считать только, что f (x) имеет производные любого порядка при x = x₀(бесконечно дифференцируема).

Составим ряд Тейлора	∞    f (n) (x0 )(x − x0 )n ∑ n=0        n!	(*)
Ниоткуда не следует, вообще говоря, что этот ряд сходится для x ≠ x0. Более того, ряд может сходится, а его сумма вовсе не равна f (x) !!!

⎧ − 1

⎪e ^x2 ,x ≠ 0    (Ряд Маклорена ≡ 0!!!)

Упр.* f (x) = ⎨

⎪⎩0,x = 0

Вопросы: 

1)  при каких условиях этот формальный ряд (*) сходится?

2)  если сходится, то будет ли его сумма S(x) совпадать с функцией f (x), его породившей?

	Теорема.	f (n) (x) ≤ M, (дост. условие разложения в ряд Тейлора).  функция f (x) и ее производные любого порядка  в окрестности точки x0:  (| x − x0 |< R)  тем же числом M :    ,....)то ее ряд Тейлора сходится к самой f (x)  x из этой окрестности | x − x0 |< R . функция f (x) разложима в ряд Тейлора, то это  единственно.
	Если ограничены одним и (n = 0,1,2 для любого  Если разложение

Обозначим T_n (x) сумму первых членов ряда Тейлора 

(n)

                                                                                                                             f      (x^{0 )           n}

T_n (x) = f (x₀ ) + f ′(x₀ )(x − x₀ ) +...+            (x − x₀ ⁾

n!

Таким образом, имеет место формула Тейлора

(n) f      (x f (x) = f (x0 )+ f ′(x0 )(x − x0 )+...+            0 )(x − x0 )n + Rn (x) n!

Важно знать,  как устроен остаток R_n (x) !!!

	Теорема.	Если функция f (x) имеет производную   порядка f (n+1) (x) в окрестности точки x0, то  член имеет вид: , некоторая точка, лежащая между x  и x0.
	(n+1)-го остаточный где  ξ -

При n = 0 из формулы Тейлора имеем   f (x) = f (x0) + f ′(ξ)(x − x0)     -формула Лагранжа  При n = 1 имеем   f ′′(ξ) f (x) = f (x0) + f ′(x0)(x − x0) +     (x − x0)2 2! Если отбросить остаточный член, то получимf (x) ≈ f (x0) + f ′(x0)(x − x0)2 - формула для вычисления приближенного значения через дифференциал

Удобно пользоваться следующей оценкой : если  производную  f ⁽ⁿ⁺¹⁾ (x) удовлетворяет условию

f (n+1) (x)

≤ M n+1,

для некоторого числа M _n+1, то 

| x − x |n+1 | Rn (x) |≤ M n+1 ⋅ 0 n +1

Выпишем теперь разложение в степенные ряды Маклорена (при x₀ = 0) некоторых элементарных функций:

1) f (x) = e^x       

Имеем                f ′(x) = e^x ,....., f ⁽ⁿ⁾ (x) = e^x ,.........

Следовательно, при  x₀ = 0

ex =1+ x + x2 +...+ xn +... 2!      n!

Найдем радиус сходимости этого ряда

                                    aⁿ |= lim       ^n!     = lim    ¹   = 0   или R = ¹ = ∞   

l = lim |

n→∞ a_n+₁        n→∞ (n +1)!   n→∞ n +1                     l

Значит, ряд в правой части сходится на всей оси   (−∞,+∞).  Если взять промежуток вида [−N,+N],  где N -произвольно, то для ∀x∈[−N, N] имеем оценку                | f ⁽ⁿ⁾ (x) |≤ e^N = M,∀n = 0,1,2,3....

Согласно теореме (достат. условие) функция f (x) = e^x разлагается в ряд Маклорена на всей оси (−∞,∞) так как N -произвольно.

Интересно заметить, что  при x = 1 получаем

1    1 e =1+1+  +...+  +... 2!          n!

2)      f (x) = sin x  

Вычислим

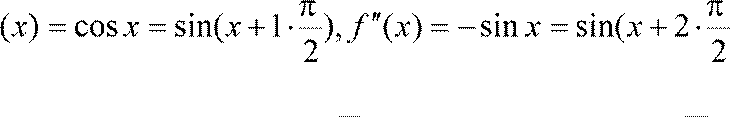f ′),

f ′′′),..., f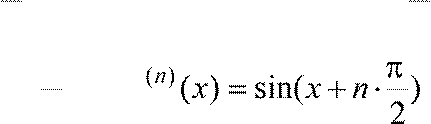

f (0) = 0, f ′(0) =1, f ′′(0) = 0, f ′′′(0) = −1,...,

Отсюда       f (2n) = 0, f (2n−1) = (−1)n−1

Тогда               

     

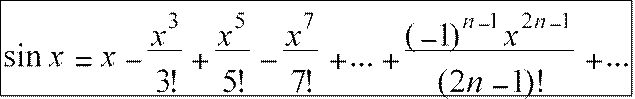
Можно показать, что радиус сходимости ряда   R = ∞

Так как | f 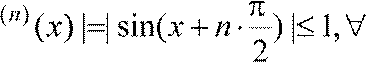x, то ряд сходится к функции sin x на всей оси.

На рис. 3 изображен жирной линией график функции

Y₁ = sin x,тонкими линиями его приближение одним членом ряда Маклорена  Y₂ =x, приближение четырьмя  отличными

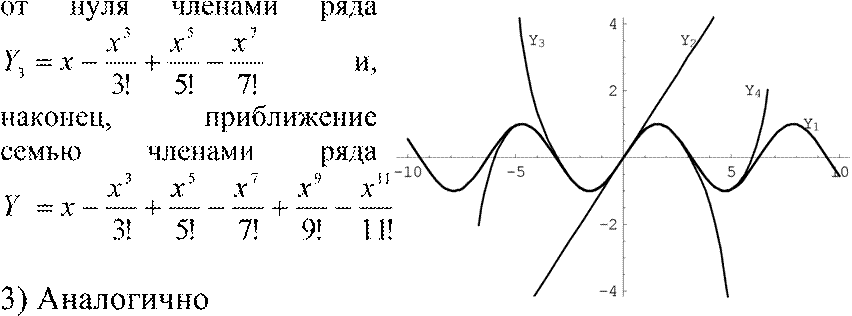4

2 4 6 n 2n x x x (−1) x cos x =1− + − +...+  +... 2!     4!     6!               (2n)!

Данные разложения верны для x∈(−∞;+∞).

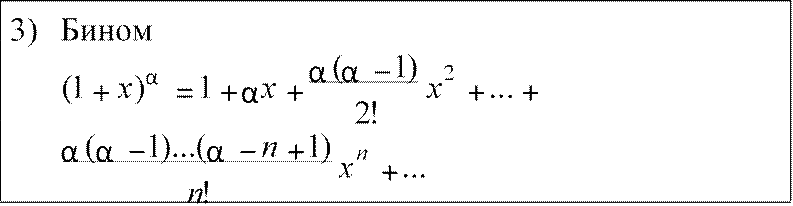
Данное разложение верно при x∈(−1;+1)и, может быть