














Пример 1
∞ 1
n−1
Дан сходящийся ряд ∑ (−1) 2 . Оценить ошибку,
n=1 n
допускаемую при замене суммы этого ряда:
1) суммой первых трех его членов
2)
 суммой
первых его четырех членов Решение.
суммой
первых его четырех членов Решение.
1) Из формулы S = Sn + rn находим S = S3 + r3 . Или
|
| rn |< an+1 |
S
=
1−
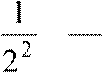 +
+ 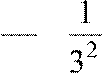 +
r3.
Откуда S =
+
r3.
Откуда S = ![]() +
r3.
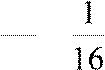
По теореме Лейбница . Значит | r3 |<
a4
или | r3 |<
+
r3.
По теореме Лейбница . Значит | r3 |<
a4
или | r3 |< 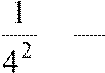 =
=
 .
.
Так
как r3 = −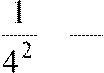 +
+  −.....+,
то r3 < 0
−.....+,
то r3 < 0
|
(см. т. Лейбница) Для ряда вида − a1 + a2 − a3 +...+ (−1)n an +..., an > 0оценка суммы ряда имеет вид − a1 < S < 0 . |
||
|
Тогда
|
S |
с избытком. |
2)
Аналогично S = S4
+
r4.
Или S 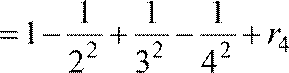 .
.
Откуда
S = ![]() +
r4.
Далее| r4 |< a5
или | r
+
r4.
Далее| r4 |< a5
или | r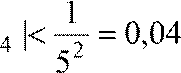 .
.
Так
как r4 = +![]() −.....+,
то r4 > 0. Значит, сумма ряда
−.....+,
то r4 > 0. Значит, сумма ряда
|
115 S ≈ 144 |
|
с недостатком
Пример 2
∞ n−1 1
Проверить, что ряд ∑ (−1) сходится.
n=1 n
 Сколько нужно взять
членов ряда, чтобы вычислить его сумму с точностью до 0,01 ?
Сколько нужно взять
членов ряда, чтобы вычислить его сумму с точностью до 0,01 ?
Решение.
1) Ряд сходится, так как все условия т. Лейбница выполнены.
|
| rn |< an+1 |
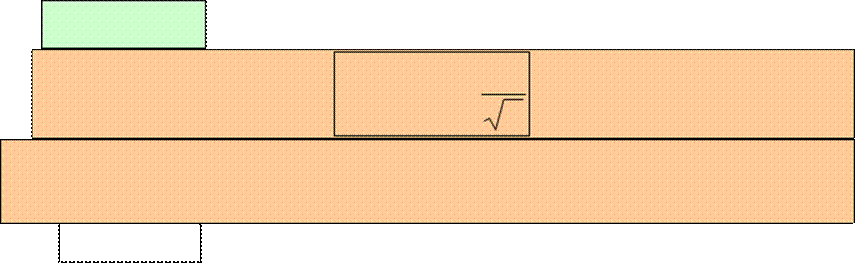
2) Так как S = Sn + rn и верна оценка , то
1
![]() требуемое
n найдем из условия: an+1
=<
0,01.
n +1
требуемое
n найдем из условия: an+1
=<
0,01.
n +1
1
![]() Из
уравнения = 0,01 находим n =
9999
n +1
Из
уравнения = 0,01 находим n =
9999
n +1
Итак, | r9999 |< 0,01 причем 0 < r9999 < 0,01. Значит
S = S9999 + r9999 или S ≈ S9999 с недостатком.
Пример 3Сколько нужно взять членов ряда
∞ n−1 n
 ∑ (−1) n
, чтобы вычислить его сумму с n=1 (2n
+1)5
точностью до 0,01 ?
∑ (−1) n
, чтобы вычислить его сумму с n=1 (2n
+1)5
точностью до 0,01 ?
1)
Ряд сходится по т. Лейбница 2) a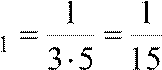 ,
a
,
a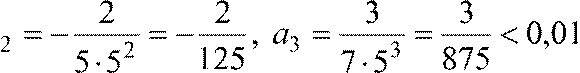 . Значит, надо взять два члена ряда
S = S2
+
r2,
или
. Значит, надо взять два члена ряда
S = S2
+
r2,
или
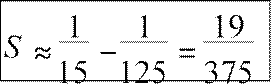 ,
(с недостатком, так r2 > 0)
,
(с недостатком, так r2 > 0)
Пример 4 Найти сумму ряда
 1+
2x
+3x2
+
4x3
+...+...(|
x |<1)
1+
2x
+3x2
+
4x3
+...+...(|
x |<1)
Применим дифференцирование степенных рядов.
Рассмотрим геометрическую прогрессию
1+
x
+
x2
+
x3
+...+...
= ![]() 1
при (| x |<1)
1
при (| x |<1)
1− x Дифференцируем этот ряд
 (1+
x
+
x2
+
x3
+...+...)′
= (
1 ′
(1+
x
+
x2
+
x3
+...+...)′
= (
1 ′
Применим интегрирование степенных рядов.
Рассмотрим геометрическую прогрессию
1+
x
+
x2
+
x3
+...+...
= ![]() 1
при (| x |<1)
1
при (| x |<1)
1− x
Интегрируем этот ряд
x 2 3 x 1
∫(1+
x
+
x
+
x
+...+...)dx
=
∫ ![]() dx.
dx.
0 0 1− x
Отсюда
x
 ),
),
Ряд сходится при −1 ≤ x < 1 !
|
k ⎛ k +1 ⎞ Здесь an =
0
при n = 2k −1
и an = ⎜ |
Находим
1 1 ⎛2k +1⎞

 R
= = =
lim ⎜ ⎟ = 2
nlim→∞
n
|
an | lim 2k
⎛⎜
k
+1
⎟⎞k k→∞ ⎝
k
+1
⎠
k→∞ ⎝2k
+1⎠
R
= = =
lim ⎜ ⎟ = 2
nlim→∞
n
|
an | lim 2k
⎛⎜
k
+1
⎟⎞k k→∞ ⎝
k
+1
⎠
k→∞ ⎝2k
+1⎠
![]() При
x − 2 = 2
имеем числовой ряд
При
x − 2 = 2
имеем числовой ряд
k
⎛ ⎞
∞ ⎛ k +1 ⎞k ⎜ k +1 ⎟ ∞ ⎛ 1 ⎞k
∞
![]() ∑
⎜
∑
⎜ ![]() ⎟ 2k
= ∑ ⎜ ⎟ = ∑ ⎜1+
⎟ 2k
= ∑ ⎜ ⎟ = ∑ ⎜1+
![]() ⎟ k=1
⎝2k
+1⎠
k=1
⎜⎜k
+ 1
⎟⎟
k=1 ⎝
2k
+1⎠
⎟ k=1
⎝2k
+1⎠
k=1
⎜⎜k
+ 1
⎟⎟
k=1 ⎝
2k
+1⎠
⎝ 2 ⎠
Так как
![]() k
k
k
⎛ 1 ⎞ ⎛ 1 ⎞
![]()
![]()
![]() lim⎜1+ ⎟ =
lim⎜1+ ⎟= e
≠
0
lim⎜1+ ⎟ =
lim⎜1+ ⎟= e
≠
0
k→∞⎝ 2k +1⎠ k→∞⎝ 2k +1⎠
то ряд расходится, ибо общий член ряда не стремится к нулю.
![]() Аналогично, при x −
2
=
− 2
ряд расходится.
Аналогично, при x −
2
=
− 2
ряд расходится.
|
Итак, |
2−
|
|
|
— область сходимости ряда |
 Среди
различных аналитических аппаратов исследования функций первое место по своей
простоте и удобству употребления занимают степенные ряды. Идея проста: функция, которую мы хотим изучить,
представляется как предел частичных сумм простейших степенных функций.
Среди
различных аналитических аппаратов исследования функций первое место по своей
простоте и удобству употребления занимают степенные ряды. Идея проста: функция, которую мы хотим изучить,
представляется как предел частичных сумм простейших степенных функций.
Пусть задана f (x) в окрестности точки x = x0 .
Предположим, что f (x) разлагается в ряд по степеням
(x − x0 ): т.е. ряд имеет вид f (x) = a0 + a1(x − x0 ) + a2 (x − x0 )2 +..+ an (x − x0 )n +...(1) с радиусом сходимости R, (| x − x0 |< R)
Этот ряд на интервале сходимости | x − x0 |< R можно дифференцировать бесконечно число раз:
f ′(x) = a1 + 2⋅a2 ⋅(x − x0 )+3⋅a3 ⋅(x − x0 )2..+ n⋅an ⋅(x − x0 )n−1...
f ′′(x) = 2⋅1⋅a2 +3⋅2⋅a3(x − x0 ) +..+ n⋅(n −1)⋅an ⋅(x − x0 )n−2...
……………………………………………………………… f (n)(x) = n⋅(n −1)⋅...⋅1⋅an + (n +1)⋅n⋅...⋅3⋅2an+1 ⋅(x − x0) +...
Положим в каждом равенстве x = x0. Тогда последовательно получаем коэффициенты Тейлора:
![]() f
′(x0
),
a = f ′′(x0
),…a
=
f
(n)
(x0
)
a0 = f (x0
) a1 = 2
n ,.
f
′(x0
),
a = f ′′(x0
),…a
=
f
(n)
(x0
)
a0 = f (x0
) a1 = 2
n ,.
1! 2! n!
Итак, если функция f (x) разлагается в ряд по степеням
(x − x0 ), то этот ряд имеет вид
|
|
||
|
f (n) (x ) ∞ (n) n
|
(2) |
|
|
Определение. |
Степенной ряд вида (2) называется рядом функции f (x) в точке x0. Если x0 = 0, то ряд f n (0) n ∞ f (n)(0) n
рядом Маклорена. |
|
|
Тейлора f (x) = f (0) + называется |
Разложение в ряд Тейлора (Маклорена) было получено в предположении, что f (x) разлагается в ряд.
Теперь откажемся от этого предположения. Будем считать только, что f (x) имеет производные любого порядка при x = x0(бесконечно дифференцируема).
|
Составим ряд Тейлора |
|
(*) |
|
Ниоткуда не следует, вообще говоря, что этот ряд сходится для x ≠ x0. Более того, ряд может сходится, а его сумма вовсе не равна f (x) !!! |
||
⎧ −
![]() 1
1
⎪e x2 ,x ≠ 0 (Ряд Маклорена ≡ 0!!!)
Упр.* f (x) = ⎨
⎪⎩0,x = 0
Вопросы:
1) при каких условиях этот формальный ряд (*) сходится?
2)
 если
сходится, то будет ли его сумма S(x) совпадать с функцией f (x),
его породившей?
если
сходится, то будет ли его сумма S(x) совпадать с функцией f (x),
его породившей?
|
(дост. условие разложения в ряд Тейлора). функция f (x) и ее производные любого порядка в окрестности точки x0: (| x − x0 |< R) тем же числом M : ,....)то ее ряд Тейлора сходится к самой f (x) x из этой окрестности | x − x0 |< R . функция f (x) разложима в ряд Тейлора, то это единственно. |
||||
|
Если ограничены одним и (n = 0,1,2 для любого Если разложение |
Остаточный член ряда Тейлора.
Обозначим Tn (x) сумму первых членов ряда Тейлора
(n)
![]() f (x0
) n
f (x0
) n
Tn (x) = f (x0 ) + f ′(x0 )(x − x0 ) +...+ (x − x0 )
n!
Остаточным членом ряда Тейлора называют разность
Rn(x) = f (x)−Tn(x)
Таким образом, имеет место формула Тейлора
|
(n) f (x
n! |
Важно знать, как устроен остаток Rn (x) !!!
|
Если функция f (x) имеет производную порядка f (n+1) (x) в окрестности точки x0, то член имеет вид:
|
||
|
(n+1)-го остаточный где ξ - |
|
При n = 0 из формулы Тейлора имеем f (x) = f (x0) + f ′(ξ)(x − x0) -формула Лагранжа При n = 1 имеем f ′′(ξ) f
(x)
=
f
(x0)
+
f
′(x0)(x
−
x0)
+ 2! Если отбросить остаточный член, то получимf (x) ≈ f (x0) + f ′(x0)(x − x0)2 - формула для вычисления приближенного значения через дифференциал |
Само по себе выражение для Rn(x) не дает возможности вычислять его величину, так как неизвестна точка ξ , в которой вычисляется f (n+1) (x).
Удобно пользоваться следующей оценкой : если производную f (n+1) (x) удовлетворяет условию
|
f (n+1) (x) |
≤ M n+1, |
для некоторого числа M n+1, то
|
| x − x |n+1 | Rn (x) |≤ M n+1 ⋅ 0 n +1 |
|
Этой формулой можно пользоваться для оценки точности аппроксимации функции f (x) ее многочленом Тейлора Tn(x).
Разложение некоторых элементарных функций в степенные ряды
Выпишем теперь разложение в степенные ряды Маклорена (при x0 = 0) некоторых элементарных функций:
1) f (x) = ex
Имеем f ′(x) = ex ,....., f (n) (x) = ex ,.........
Следовательно, при x0 = 0
|
ex
=1+
x
+
|
Найдем радиус сходимости этого ряда
![]()
![]()
![]()
![]() an |=
lim n! =
lim 1 =
0
или R = 1 =
∞
an |=
lim n! =
lim 1 =
0
или R = 1 =
∞
l = lim |
n→∞ an+1 n→∞ (n +1)! n→∞ n +1 l
Значит, ряд в правой части сходится на всей оси (−∞,+∞). Если взять промежуток вида [−N,+N], где N -произвольно, то для ∀x∈[−N, N] имеем оценку | f (n) (x) |≤ eN = M,∀n = 0,1,2,3....
Согласно теореме (достат. условие) функция f (x) = ex разлагается в ряд Маклорена на всей оси (−∞,∞) так как N -произвольно.
Интересно заметить, что при x = 1 получаем
|
1 1 e =1+1+ 2! n! |
2) f (x) = sin x
Вычислим
f
′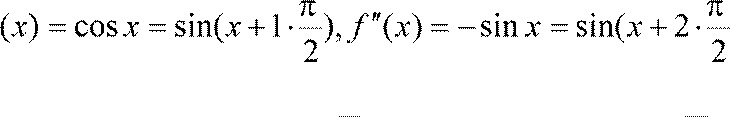 ),
),
f
′′′ ),...,
f
),...,
f 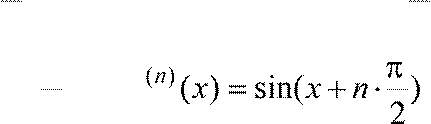
f (0) = 0, f ′(0) =1, f ′′(0) = 0, f ′′′(0) = −1,...,
Отсюда f (2n) = 0, f (2n−1) = (−1)n−1
Тогда
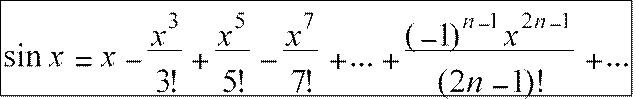
Можно показать, что радиус сходимости ряда R = ∞
Так
как | f 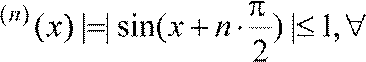 x,
то ряд сходится к
функции sin x на всей оси.
x,
то ряд сходится к
функции sin x на всей оси.
На рис. 3 изображен жирной линией график функции
Y1 = sin x,тонкими линиями его приближение одним членом ряда Маклорена Y2 =x, приближение четырьмя отличными
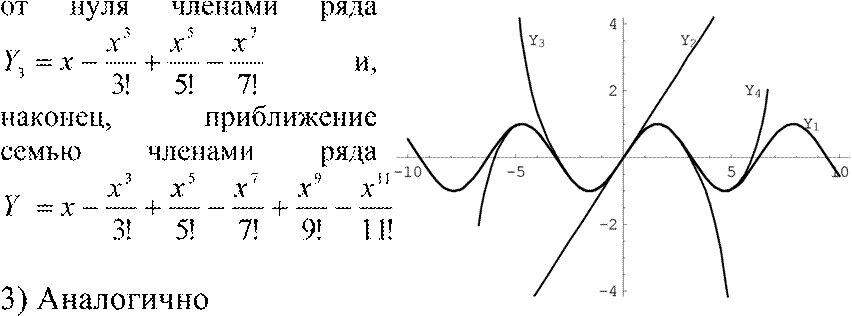 4
4
|
2! 4! 6! (2n)! |
Данные разложения верны для x∈(−∞;+∞).

Данное разложение верно при x∈(−1;+1)и, может быть
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.