Линейные дифференциальные уравнения 2-го порядка. Задачи Коши

1. Задачи Коши.  Общее решение    ЛДУ 2-го порядка

	Определение1	Дифференциальное уравнение вида ′ + B(x)y′ + C(x)y = f (x),            (1)                   B(x),C(x), f (x) − функции, заданные в области      D ⊂ R, называется линейным  уравнением второго порядка.
	A(x)y′ где A(x) ≠ 0, некоторой дифференциальным

Если A ≠ 0,B,C −константы, то ДУ (1) называется уравнением с постоянными коэффициентами;  если f (x) ≡ 0, то линейным однородным;  если f (x) ≠ 0, то линейным неоднородным.

	Задача Коши			: Для заданных начальных условий где x0 ∈ X ⊂ D, X − промежуток  функций A(x) ≠ 0, B(x), C(x), f (x), а произвольные числа, требуется найти такое (x) уравнения (1), чтобы    y0 =ϕ(x0),     y0′ =ϕ′ (x0).
	′ (x0, y0, y0 ), непрерывности y0, y0′ − решение y =ϕ
	Определение 2.				Общим решением уравнения (1) семейство функций y =ϕ (x,C1,C2),  дифференцируемое по x при :
	называется   дважды непрерывно x∈(a,b), которое
		1)  является решением уравнения (1) для любых C1,C2 из некоторой области G; 2)  обеспечивает решение задачи Коши для любых начальных условий (x0 ∈ X, y0, y0′ ) при некоторых C10 ,C20 ∈G.
	Свойства решений линейных однородных уравнений.
	Теорема 1.		Если y = y1(x) − решение уравнения (1), то = C y1(x), где C −любое постоянное число,  решением уравнения (1). Если                y = y1(x) и y = y2(x) −два решения (1), то и y = C1y1(x) +C2 y2(x), где C1,C2 −  числа, тоже решение уравнения (1).
	Теорема функция y также будет  2. уравнения произвольные

Док-во—непосредственная подстановка в ДУ !

ЦЕЛЬ—установить вид общего решения ЛДУ-2

Трудность  в обеспечении условия 2)  в Опр.2 ! 

Эти условия гарантирует    свойство линейной независимости

Определение1. Два решения y₁(x) и y₂(x) уравнения (1) называются  линейно зависимыми на интервале (a,b), если существуют числа α₁,α₂, не равные одновременно нулю, такие что α₁y₁(x) +α₂ y₂(x) ≡ 0 для всех x∈(a,b). В противном случае, функции называются линейно независимыми.  

Замечание. Две        функции       являются линейно независимыми, если их отношение не равно тождественной постоянной: y^1(x) ≠ const.  y₂(x)

Как проверить ЛНЗ ?

Важную роль играет определитель Вронского.

Пусть y1(x), y2(x)—две дифференцируемые функции. y1(x)   y2(x) Тогда определитель вида    W(x) = det y1′(x)   y2′ (x) называют определителем Вронского (аналогично n > 2

Пример.  Функции   x,sin x,cos x—ЛНЗ ?

x   sinx     cosxx   sinx     cosx

W(x) =1   cosx    -sinx       = 1   cosx    -sinx=   

0   -sinx   -cosxx     0            0

= −x(sin² x + cos² x) = −x ≠ 0 ∀x∈(a,b),a ≠ b⇒ЛНЗ  !

Упр*.  Функции  1,x²,x³—ЛНЗ ?

Какая связь Вронскиана и ЛНЗ ?

	Теорема 3.	Если дифференцируемые на(a,b) функции x) линейно зависимы (ЛЗ), то   W(x) ≡ 0    ∀x∈(a,b)
	y1(x) и y2(

	Следствие (достаточное условие ЛНЗ).	Если функции (a,b)
	W(x0) ≠ 0 хотя бы в одной точке из (a,b), то  y1(x) и y2(x) линейно независимы (ЛНЗ) на

Какое отношение к ДУ ?

Теорема 4. Для того, чтобы два частных решения  y₁(x) и y₂(x) ДУ (1) были линейно независимы

(ЛНЗ) на   (a,b)   ⇔   W(x) ≠ 0 хотя бы в одной точке    x∈(a,b)

Теорема 5 (структура общего решения). 

1)  Всякое ЛДУ (1) имеет ровно два линейно независимых решения.

2)  Если решения y₁(x) и y₂(x) уравнения (1) линейно   независимы,        то    решение y = C₁y₁(x) + C₂ y₂(x), где C₁,C₂ произвольные

постоянные, является общим решением.

Как построить два ЛНЗ решения для ДУ?

Мы найдем для частных случаев ЛДУ

Рассмотрим    ЛДУ       вида     y′′ + py′ + qy = 0,     (2)                 где p и q −постоянные числа.
Будем искать решение в виде (Эйлер)	y(x) = eλx

Подставим в ДУ (2):  ⇒ y′(x) = λe^λx, y′′(x) = λ²e^λx ⇒

⇒ y′′+ py′+ q = (λ² + pλ + q)⋅e^λx = 0 ⇒ ⎯^e⎯^λx≠⎯⁰→   

(Очевидным образом составляется по коэффициентам  Для квадратного уравнения  (3) возможны случаи:

1. Если D = p² − 4q > 0,  т.е. если  (3) имеет два различных действительных корня λ₁ и λ₂, то ДУ (2) имеет общее решение вида

y = C1eλ1x +C2eλ2x;

Док-во. Покажем, что y₁(x) = e^λ1x и y₂(x) = e^λ2x ЛНЗ ?

Вронскиан:

                                         ^{eλ1x        eλ2x}_λ1x            λ2x1        1

W(x) == e                                            ⋅e=

λ1eλ1x   λ2eλ2xλ1    λ2

= e^(λ1+λ2)x(λ₂ −λ₁) ≠ 0    ∀x∈ R ⇒ ЛНЗ

Пример1.

Найти  общее решение  для y′′ − 5y′ + 6y = 0 . Решение. Характеристическое уравнение имеет вид:λ² − λ5 + 6 = 0,  D = 25 − 24 +1 > 0.   

Значит, .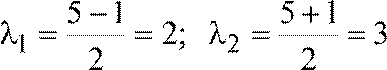 

Общее решение имеет вид: y = C₁e^2x + C₂e^3x.

2. Если D = p² − 4q = 0,  т.е. если (3) имеет два равных

− p

действительных корня λ₁ = λ₂=λ = , то ДУ (2)

2

имеет общее решение 

y = (C1 +C2x)⋅eλx

;     

λ x

Док-во.  Ясно, что y₁(x) = e            есть частное решение. 

Где взять еще одно частное решение?

λ x

Выберем в виде y(x) = x⋅e .  Тогда y′(x) = e^λx + λxe^λx, y′′(x) = 2λe^λx + λ²xe^λx ⇒         

y′′+ py′+ q = xe^λx(λ² + pλ + q) + e^λx(2λ + p) = 0 ⇒                

λ x

Действительно, y(x) = x⋅e —решение ДУ. Проверим ЛНЗ: Вронскиан:

e^λx             x e^λx_λx1            x

W(x) == e=

λeλx     xλeλx + eλx λ      xλ +1

= e^λx(xλ +1−λx) = e^λx ≠ 0    ∀x∈ R ⇒ ЛНЗ

Пример2.

Общее решение ДУ  y′′ −10y′ + 25y = 0.

Характеристическое уравнение: λ² −10λ + 25 = 0, D =100 −100 = 0, значит, λ₁ = λ₂=5. 

Тогда       y = (C₁ + C₂x)e^5x— общее решение.

3. Если D = p² − 4q < 0,  т.е. если (3) имеет два комплексно-сопряженных   корня