Теоретичні дослідження, визначення коефіцієнтів фактичної та суб’єктивної безпеки, страница 2

б) побудова математичної моделі;

в) дослідження системи на моделі і прогнозування й управління оригіналом за результатами цих досліджень.

Метод математичного моделювання, який зводить дослідження явищ зовнішнього світу до математичних задач, дозволяє проектувати нові технічні засоби, що працюють в оптимальних режимах, для розв’язання складних задач науки і техніки; передбачати нові явища.

Створення математичної моделі залежить від варіанта вихідної ситуації, тобто обсягу початкової інформації, мети і засобів моделювання.

При моделюванні технічних систем можливі такі випадки:

а) система добре вивчена, що дозволяє записати її математичну модель у вигляді аналітичних співвідношень, всі коефіцієнти яких відомі. В цьому випадку під час побудови моделі відсутні перші 2 етапи і зворотні задачі на 3-му етапі.

б) математична модель взагалі відома у вигляді аналітичної залежності, але деякі з коефіцієнтів її невідомі – побудова моделі починається з етапу 3, власне з розв’язання зворотних задач.

в) відомо, що моделлю виступає функція певного виду, яка задається у неявному вигляді (наприклад, диференційними рівняннями у частинних похідних), тому слід визначити мінімальну кількість експериментів для дискримінації моделі; моделювання починається з 2-го етапу, на якому випускають лише вибір способу представлення моделі.

г) аналітичний вигляд моделі невідомий. Побудова моделі проходить повністю всі 4 етапи.

Використання математичних моделей є одним із основних методів наукового дослідження. Основними перевагами є те, що математичне моделювання:

а) дає змогу на основі одного пристрою здійснити розв’язання цілого класу задач, які мають однакові або подібні математичні описи;

б) забезпечує простоту переходу від однієї задачі до іншої;

в) дає можливість моделювати частинами (тобто декомпонувати систему на частини, моделювати кожну частину окремо і об’єднувати моделі, що відповідають різним підсистемам чи аспектам опису), що особливо важливо під час моделювання складних транспортних систем;

г) прискорює моделювання за рахунок використання швидкодійної електронно-обчислювальної техніки;

д) вимагає менших витрат внаслідок відсутності необхідності побудови великої кількості фізичних моделей і заміни суттєвої частки емпіричних досліджень теоретичними [15].

2.4 Визначення коефіцієнтів фактичної та суб’єктивної безпеки руху

У вільних умовах руху основним і визначальним фактором, що впливає на вибраний водієм режим і траєкторію руху, є ширина проїзної частини дороги або, точніше, та її частина, що відведена для руху одного автомобіля в одному напрямку (смуга руху).

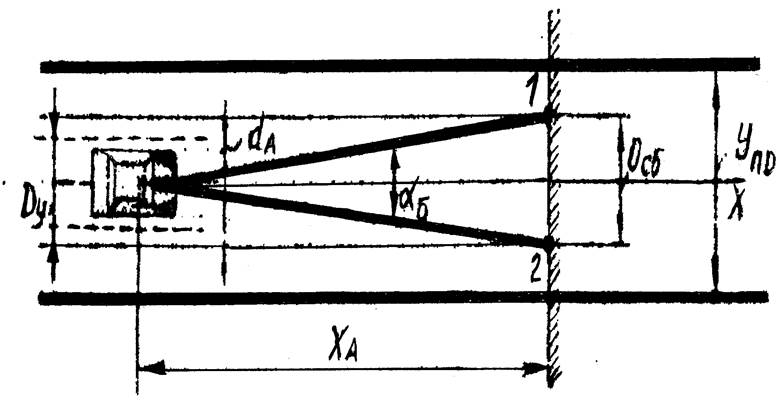
Так, якщо припустити, що автомобіль рухається по дорозі зі смугою руху, рівної У_ПД (рис. 2.1), зі швидкістю V [9], то просторове положення і можливу динаміку його зміни може бути охарактеризована наступними параметрами:

Умовні позначення:

- ширина смуги руху, м;

- фактична величина динамічного коридору, займаного автомобілем, м;

- суб’єктивний динамічний коридор автомобіля, обумовлений величиною відповідної сторони трикутника безпеки, м.

Рисунок 2.1 - Розрахункова схема при аналізі можливих швидкісних режимів руху

- фактичним динамічним коридором (Д_Ф ), що представляє собою частину смуги руху, що займає автомобіль що має геометричну ширину d_А внаслідок наявності реальних умовах руху постійних поперечних переміщень; щодо теоретичної траєкторії руху, величина яких залежить від характеристики підвіски, шин, стабільності роботи системи рульового керування автомобіля, а так само стану поверхні дороги;

– суб'єктивним динамічним коридором ( Д_СБ), що представляє собою частину смуги руху, суб'єктивно резервований водієм з метою забезпечення безпеки руху, величина якого визначається просторовим положенням опорних крапок (т.1, 2), отриманих перетинанням утворюючого кута безпеки (₎ лінією границі зони нерухомо сприйманих об'єктів, вилученої від автомобіля, на відстані Х_А [18].