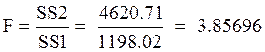
Число степеней свободы числителя и знаменателя равно
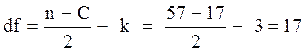
Табличное значение F-критерия:
Fтабл = 2.271893.
Расчетное значение F-критерия больше табличного, гипотеза о гомоскедастичности остатков отклоняется.
Проверка гомоскедастичности остатков по фактору x4 (длительность работы у данного работодателя)
Отношение остаточных сумм квадратов 3.610058449
Число степеней свободы 17
Табличное значение F-критерия 2.271892889
Расчетное значение F-критерия больше табличного, гипотеза о гомоскедастичности остатков отклоняется. Ввиду гетероскедастичности остатков необходимо применить обобщенный метод наименьших квадратов (ОМНК) для корректировки модели.
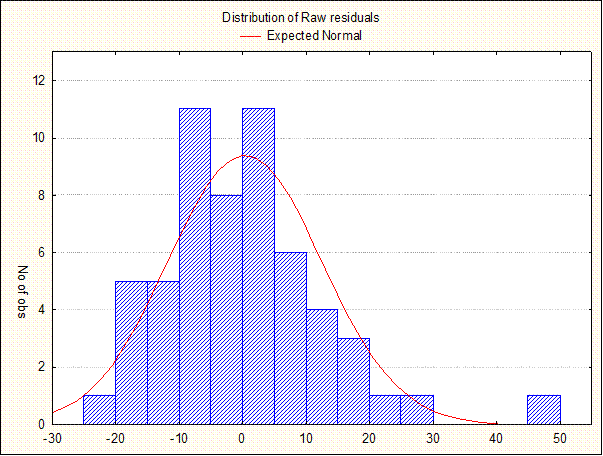
Графики остатков, полученные с помощью пакета STATISTICA
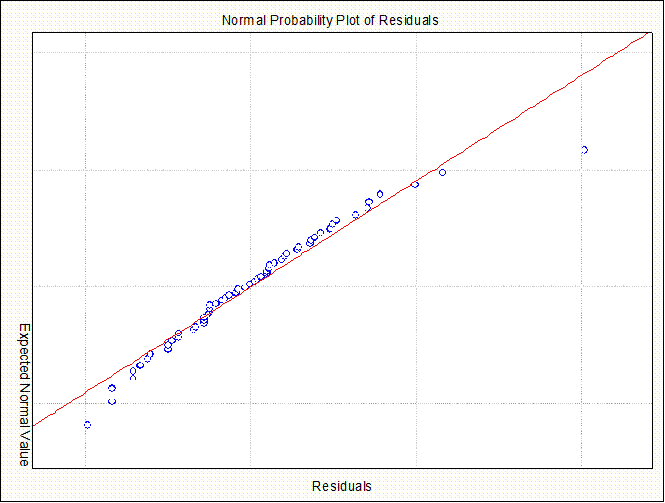
Остатки расположены вблизи прямой на нормальном вероятностном графике. Это указывает на то, что закон распределения остатков близок к нормальному. Об этом же свидетельствует и гистограмма остатков с наложенной нормальной кривой.
Тест Колмогорова-Смирнова для проверки гипотезы о нормальном законе распределения остатков

Если вычисленная статистика D (расхождение между теоретическим и выборочным законами распределения) значима, то строка имеет красный цвет и гипотеза о том, что анализируемые данные имеют нормальный закон распределения, должна быть отвергнута.
В данном случае нет оснований отклонить гипотезу о нормальном распределении остатков: с вероятностью более 20% расхождение между теоретическим и выборочным распределениями остатков обусловлены случайными факторами.
Тест Дарбина-Уотсона для проверки автокорреляции остатков

Значение критерия Дарбина-Уотсона, близкое к 2, позволяет сделать вывод об отсутствии автокорреляции в остатках. Об этом же свидетельствует величина коэффициента автокорреляции остатков -0.1095, которая по модулю меньше критического значения 0,2639 (см. стр. 189 Практикума Елисеевой И.И.).
Обобщенный метод наименьших квадратов
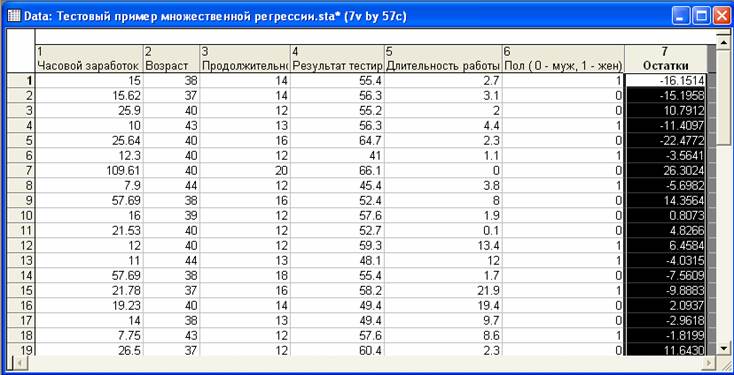
Исходная модель
Дисперсия остатков пропорциональна x2

Дисперсия остатков пропорциональна квадрату x2
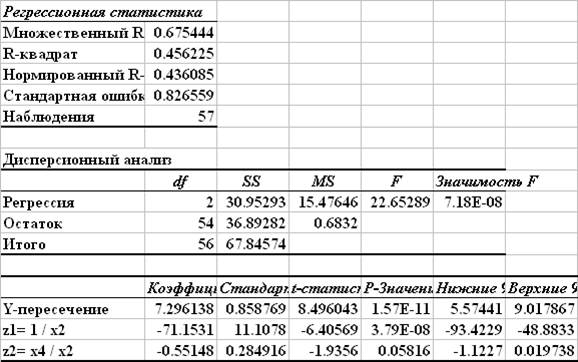

Дисперсия остатков пропорциональна x4
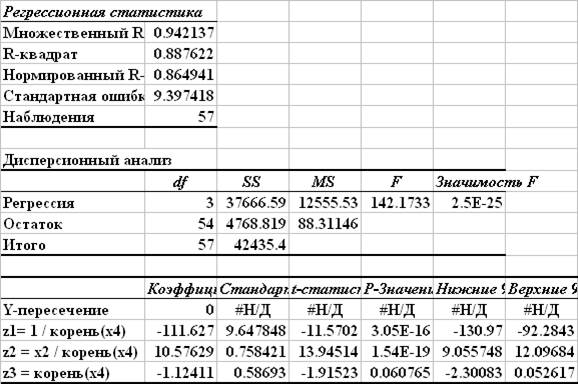

Дисперсия остатков пропорциональна квадрату x4
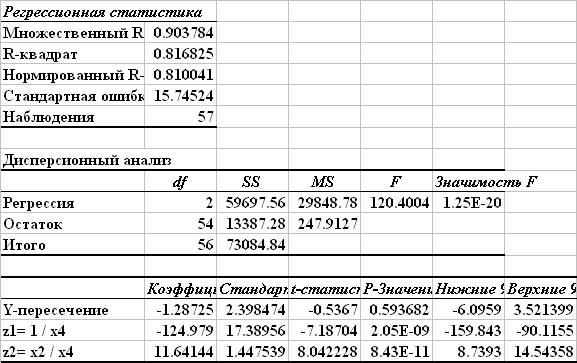

Дисперсия остатков пропорциональна расчетному значению y
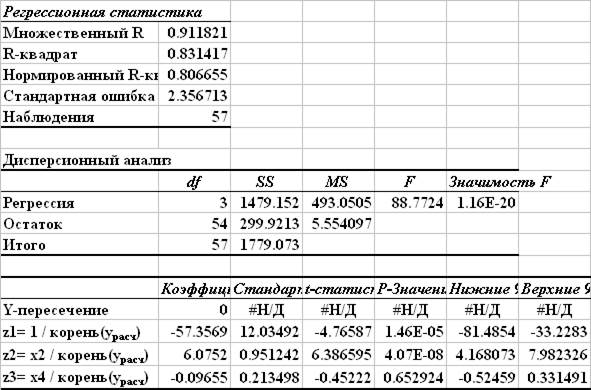

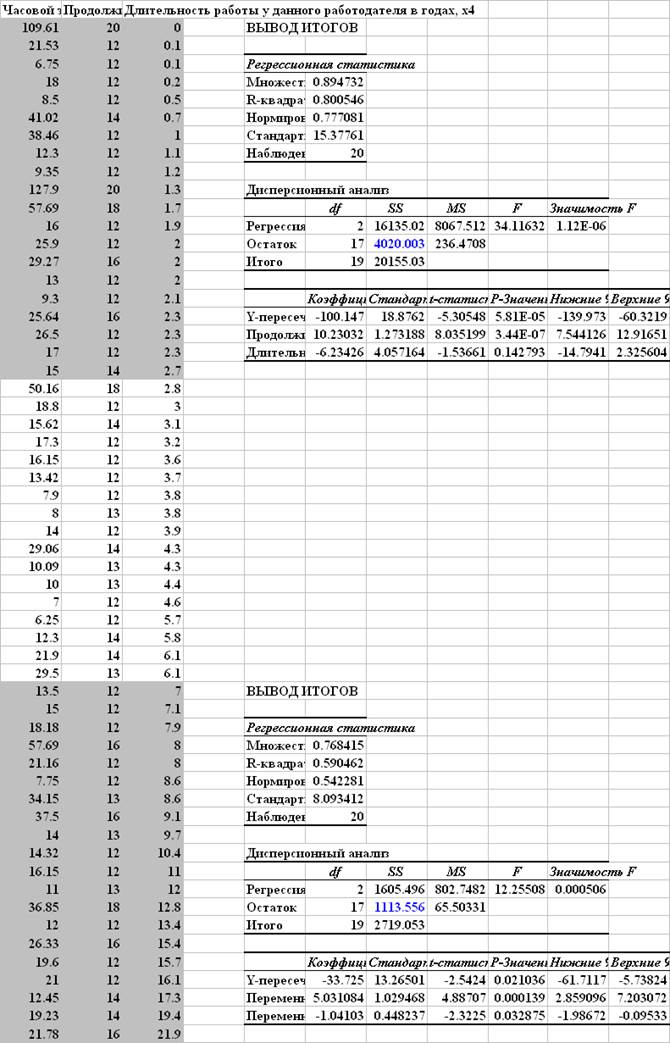
Сводная таблица результатов расчетов
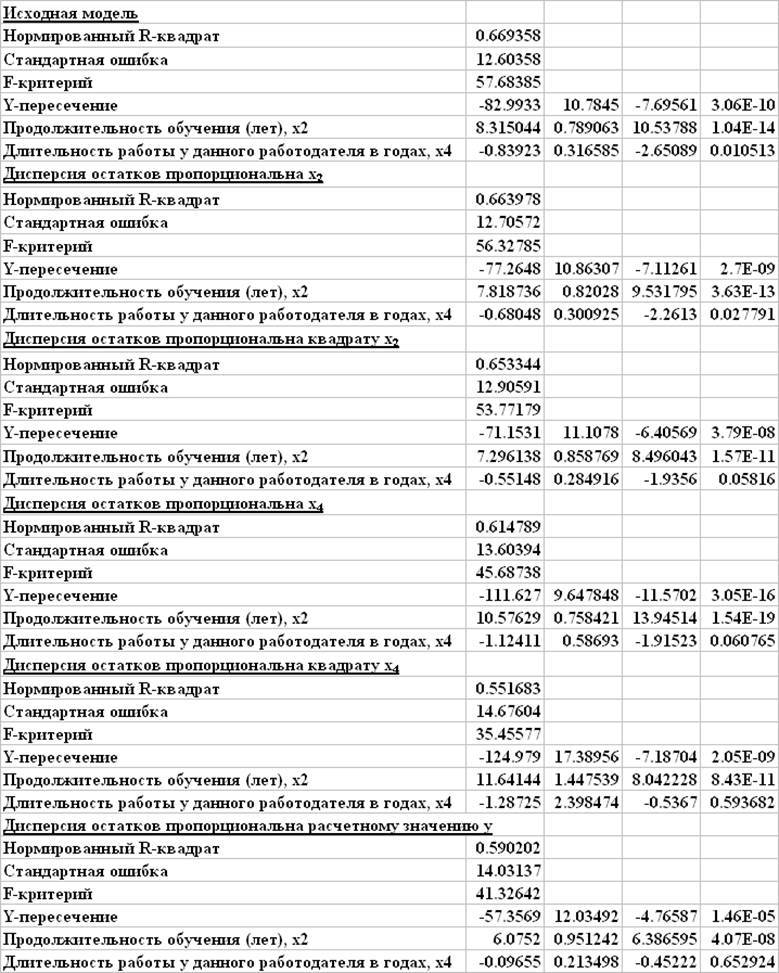
Из рассмотренных 5 моделей выбирается первая модель, построенная в предположении, что дисперсия остатков пропорциональна x2 - продолжительности обучения. В отличие от других моделей выбранная модель не содержит незначимых факторов.
Матричные вычисления для ВМНК (дисперсия остатков пропорциональна x2)
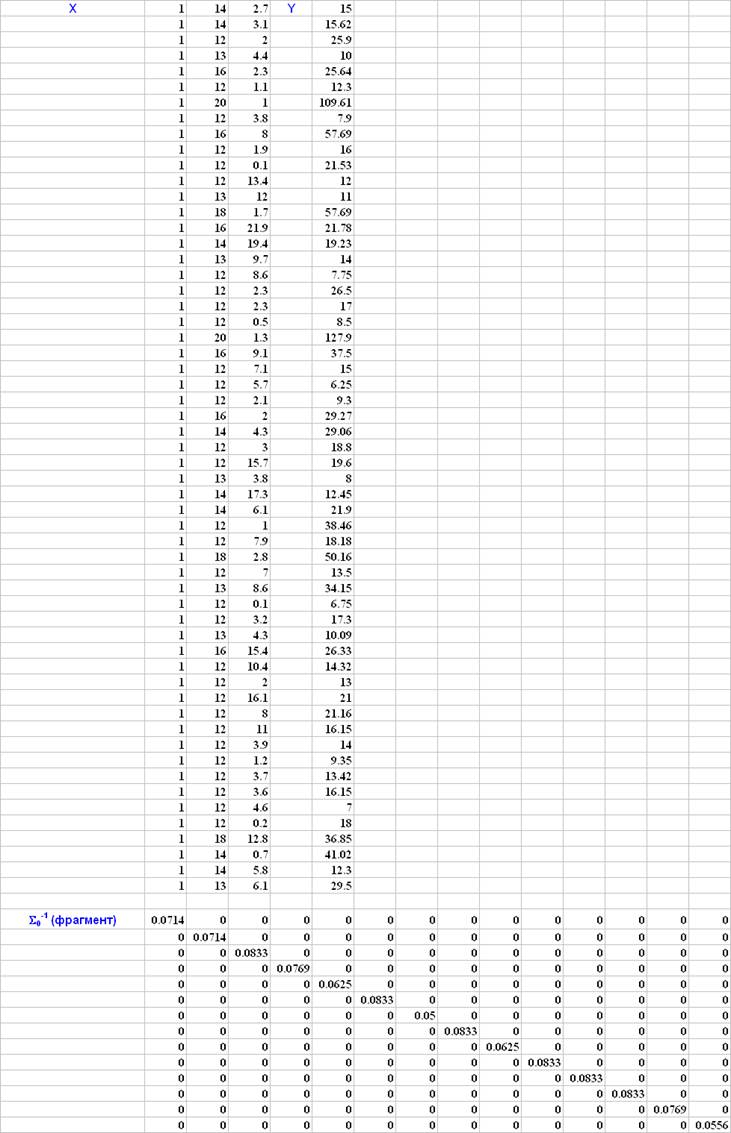
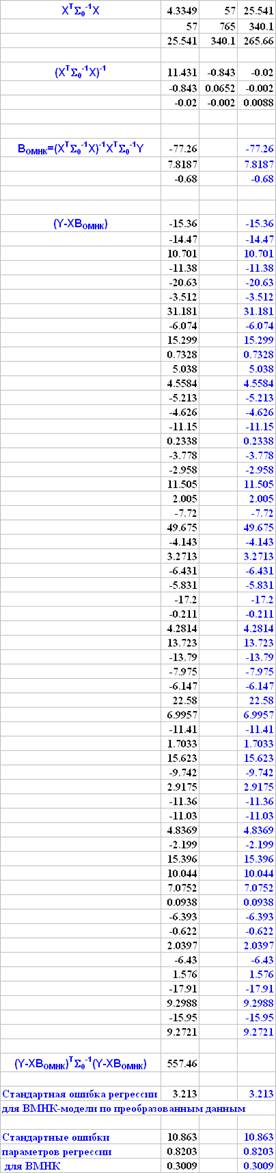
Результаты матричных вычислений совпадают с параметрами модели, полученной по преобразованным данным.
Общие результаты применения ВМНК
Исходная модель, полученная стандартным МНК:
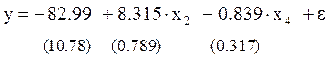
В скобках указаны стандартные ошибки параметров регрессии.
Для
исходной модели скорректированный коэффициент детерминации равен ![]() .
.
Стандартная ошибка регрессии Sост = 12.60.
Для исходной модели нарушается предпосылка МНК о гомоскедастичности остатков.
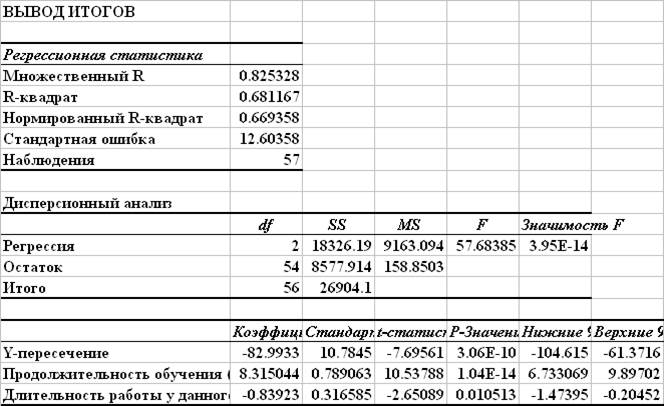
Модель, построенная ВМНК по преобразованным значениям в предположении, что дисперсия остатков исходной модели пропорциональна фактору x2 - продолжительности обучения:
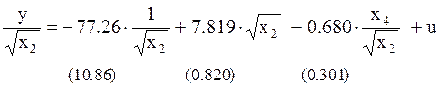
u – случайный остаток.
Для
этой модели скорректированный коэффициент детерминации равен ![]() .
.
Стандартная ошибка регрессии Sост = 3.213.
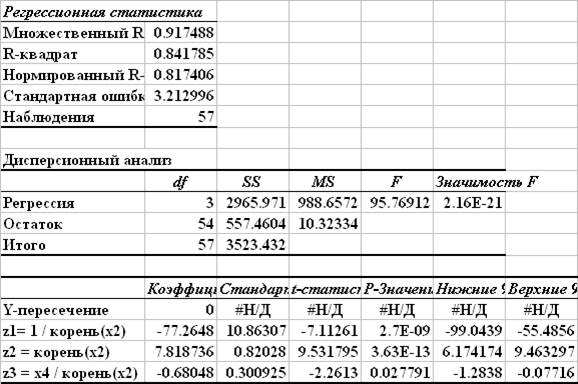
Недостатком данной модели является невозможность ее экономической интерпретации. Поэтому выполняется обратный переход к исходным значениям показателей:
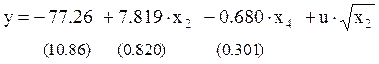
Для данной модели
скорректированный коэффициент детерминации равен ![]() .
.
Стандартная ошибка регрессии Sост = 12.71.
Модель, полученная с помощью ВМНК, по своим характеристикам близка к исходной модели, но оценки ее параметров обладают оптимальными свойствами (являются несмещенными, эффективными и состоятельными).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.