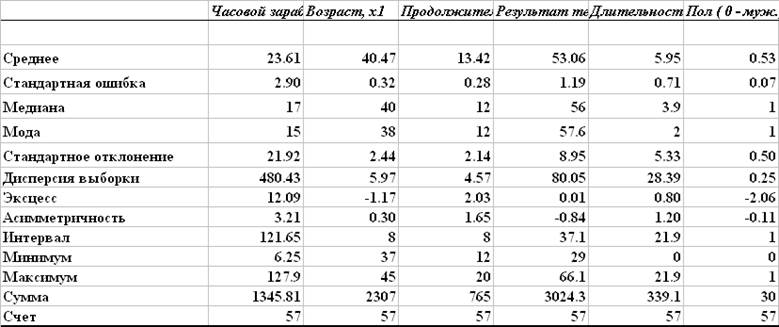
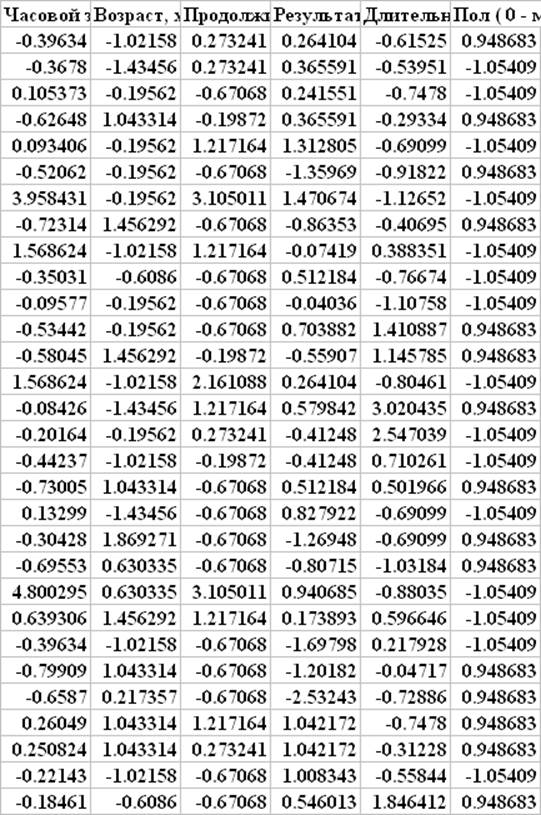
Описательные статистики для выборки после удаления аномальных наблюдений
|
Коэффициенты вариации: |
|
|
ny |
92.8% |
|
nx1 |
6.0% |
|
nx2 |
15.9% |
|
nx3 |
16.9% |
|
nx4 |
89.6% |
|
nx5 |
95.7% |
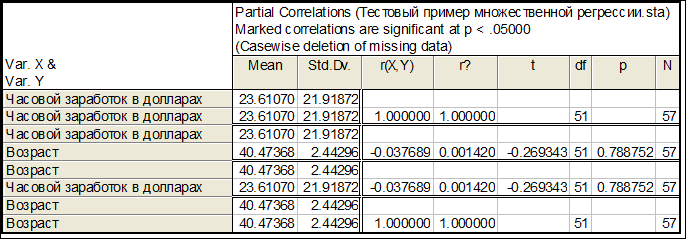
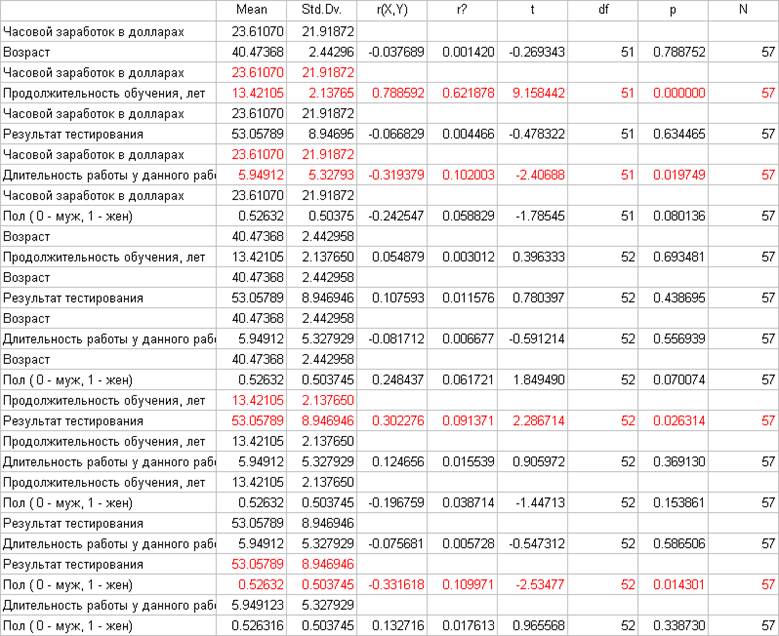
Коэффициенты парной корреляции
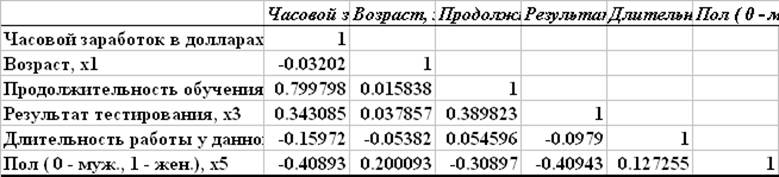
Значения коэффициентов парной корреляции указывают на тесную связь часового заработка y с продолжительностью обучения x2 и умеренную связь y с результатами тестирования x3 и полом работника x5. В то же время имеет место умеренная связь между этими двумя факторами, а также между ними и продолжительностью обучения x2, поэтому следует рассмотреть коэффициенты частной корреляции, которые дают более точную характеристику тесноты связи анализируемых признаков.
Полная матрица коэффициентов парной корреляции
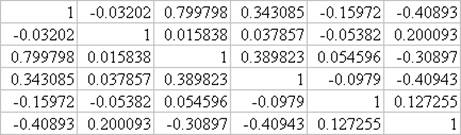
Коэффициент множественной корреляции
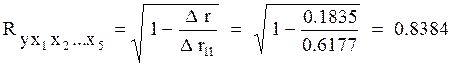
Dr -определитель полной матрицы коэффициентов парной корреляции;
Dr11 -определитель матрицы межфакторных коэффициентов парной корреляции.
Линейные коэффициенты частной корреляции (вычислены пакетом STATISTICA и в ЭТ Excel)
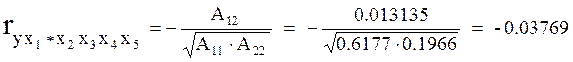

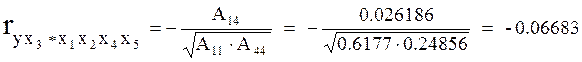
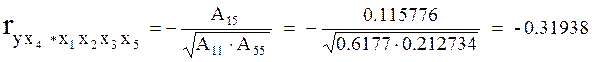
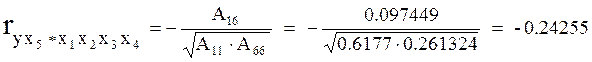
Аij - алгебраическое дополнение (i, j)-го элемента корреляционной матрицы.
Коэффициенты частной корреляции подтверждают сделанный ранее вывод относительно тесной связи часового заработка y с продолжительностью обучения x2, но опровергают наличие существенной связи y с результатами тестирования x3. Наряду со значимым частным коэффициентом корреляции y с x2 (значение t-критерия более 9; P-значение практически равно нулю) значимым является также частный коэффициент корреляции y с x4 - длительностью работы у данного работодателя (значение t-критерия по модулю равно 2.4; P-значение меньше 2%).
Таким образом, факторы x2 и x4 являются главными претендентами для включения в модель множественной регрессии. Не исключается целесообразность включения в модель множественной регрессии фактора x5 - пол работника, частный коэффициент корреляции которого с y является значимым на уровне 8%.
Наличие значимых частных коэффициентов между факторами (x2 и x3; x3 и x5) обусловливает необходимость учета мультиколлинеарности факторов при построении модели множественной регрессии.
Построение модели множественной регрессии с помощью пакета «Анализ данных»
Уравнение множественной линейной регрессии в стандартизованной форме

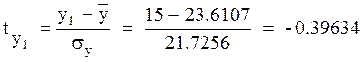
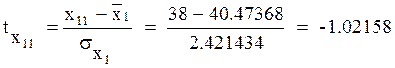
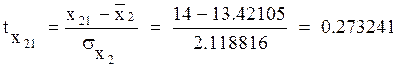
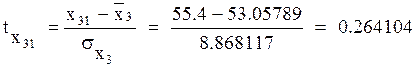
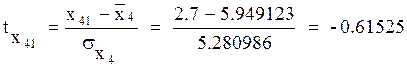
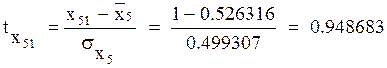
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.