Множественная регрессия. Предварительная обработка данных. Удаление наблюдений по максимуму приращения коэффициента детерминации, страница 7

Средние коэффициенты эластичности характеризуют  относительный прирост в процентах результативного показателя при изменении фактора на 1%. Коэффициенты стандартизованной регрессии характеризуют  относительный прирост результативного показателя, выраженный в среднеквадратических отклонениях, при изменении фактора на одно среднеквадратическое отклонение. Поэтому значения этих коэффициентов одинаковы по знаку.

Модель множественной линейной регрессии с полным набором факторов

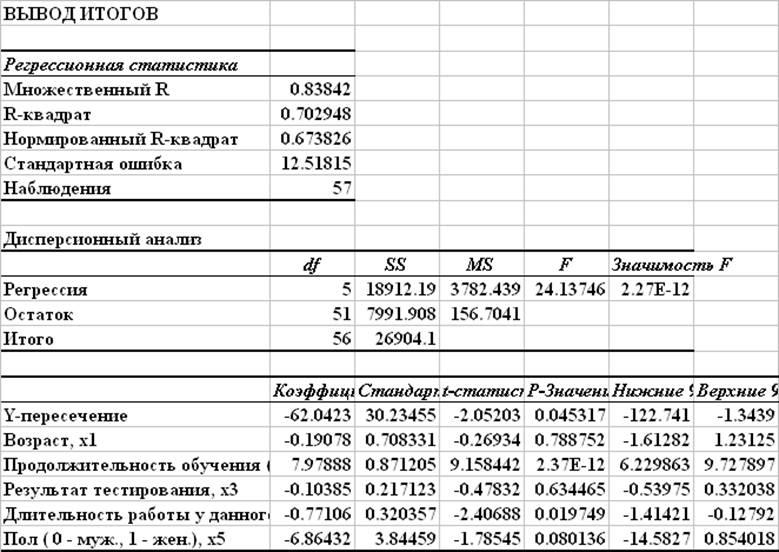
В модели с полным набором факторов имеются статистически незначимые факторы, для которых P-значение превышает уровень значимости 5%:                               

Возраст, x₁               

Результат тестирования, x₃            

Пол ( 0 - муж., 1 - жен.), x₅            

Эти факторы должны последовательно исключаться из модели. При выборе очередного исключаемого фактора следует учитывать как уровень значимости, так и вклад фактора в мультиколлинеарность.                            

Анализ мультиколлинеарности факторов

Матрица парных коэффициентов корреляции между факторами:

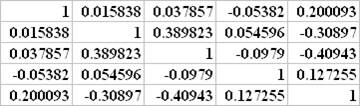
Определитель матрицы парных коэффициентов корреляции между факторами равен 0.6177. Величина определителя матрицы межфакторных коэффициентов корреляции существенно отличается от нуля, что свидетельствует о слабой степени мультиколлинеарности факторов. Для уточнения вклада каждого фактора в мультколлинеарность рассчитываются коэффициенты множественной детерминации.                                                                                                       

Коэффициенты множественной детерминации

для x₁

для x₂

 

для x₃

для x₄

для x₅

Высокое значение определителя матрицы межфакторных корреляций (0,6177) и низкие значения коэффициентов множественной детерминации для всех факторов (0.258 и менее) свидетельствуют об отсутствии мультиколлинеарности факторов.

В данном случае при формировании модели множественной регрессии с информативными факторами необходимо учитывать только значимость факторов - вклад каждого фактора в объясненную долю дисперсии часового заработка y.  

Для оценки значимости фактора можно применять любой из трех критериев:    

• частный коэффициент корреляции;
• t-критерий Стьюдента (или P-значение) для соответствующего коэффициента регрессии;
• частный F-критерий Фишера.

Формирование модели регрессии с информативными факторами

Выше было показано, что фактору x₁ (возраст работника) соответствует наименьшая по модулю, незначимая величина частного коэффициента корреляции -0.03769 (P-значение равно 0.78875). Коэффициенту регрессии этого фактора в модели с полным набором факторов соответствует наименьшая по модулю величина t-критерия Стьюдента (-0.2693) с тем же P-значением. Следовательно, фактор x₁ (возраст работника) в первую очередь должен быть исключен из модели множественной регрессии.          

Модель без фактора х₁

 

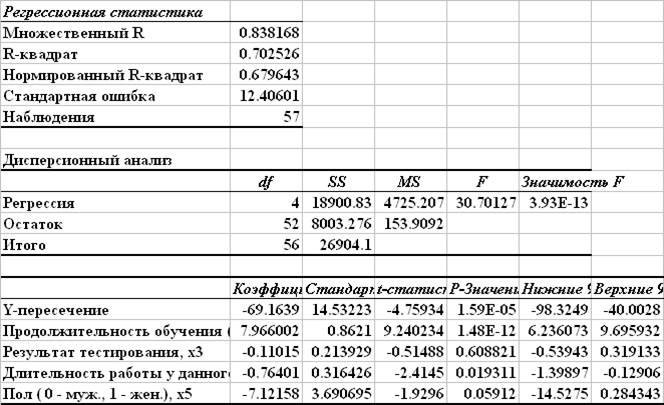
Проверка целесообразности исключения из модели фактора x₁ по частному F-критерию:

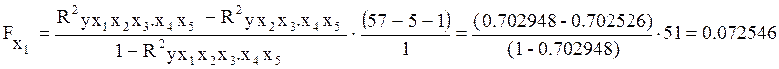
Табличное значение F-критерия    F_табл(0,05;1;51) = 4.0304.

Расчетное значение частного F-критерия для фактора x₁ меньше табличного. Включение в модель фактора x₁ нецелесообразно.       

Дальнейшее исключение из модели незначимых факторов проводится по t-критерию Стьюдента (P-значению). Из 4-факторной модели исключается фактор x₃ - результат тестирования, которому соответствует наименьшая по модулю величина t-критерия  -0.51488 (наибольшее P-значение 0.6088).         

Модель регрессии после исключения факторов x₁ и x₃  .

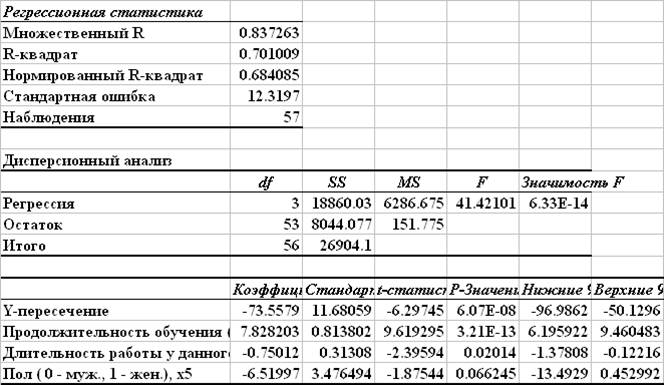
Далее из модели удаляется незначимый фактор x₅ - пол работника, для которого P-значение 0.066245 > 0.05, в результате получена двухфакторная модель, включающая только значимые факторы.