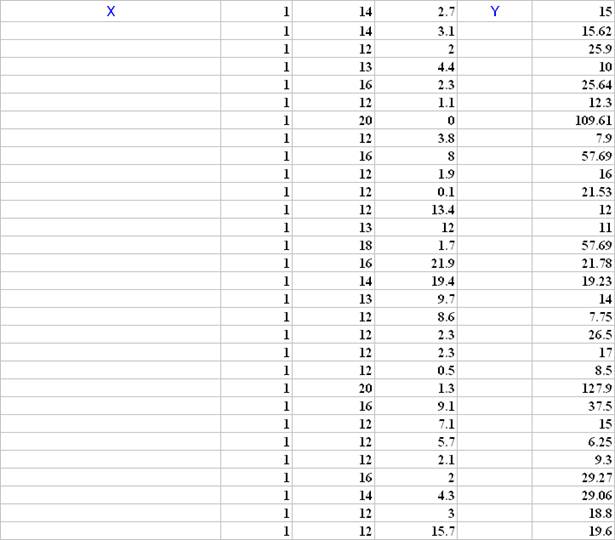
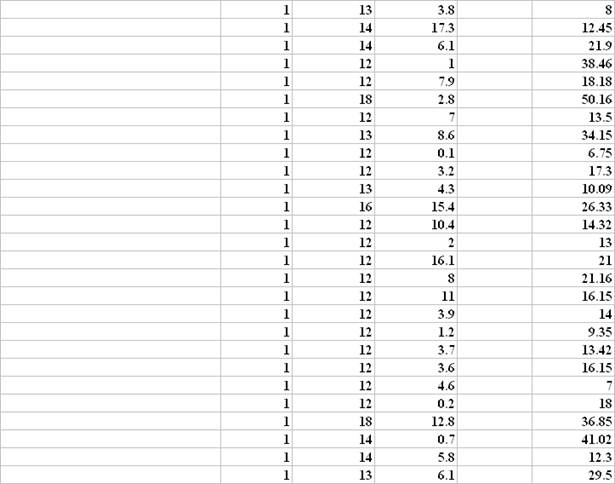
Модель регрессии, включающая только значимые факторы: x2 - продолжительность обучения и x4 - длительность работы у данного работодателя
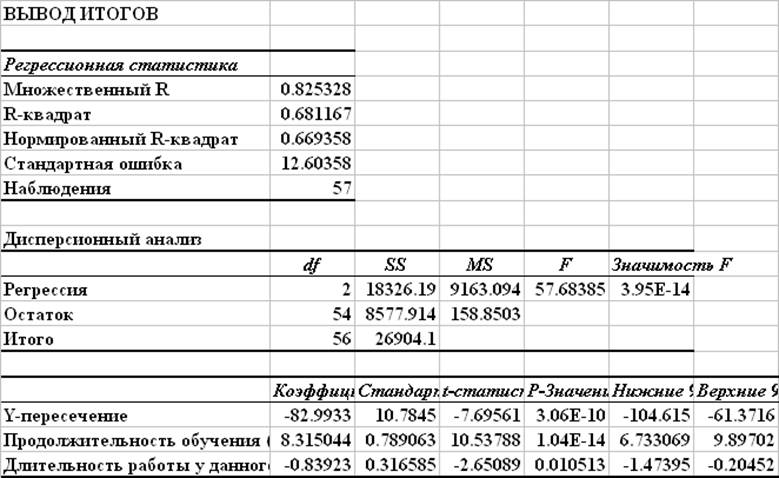
Показатели качества полученной модели регрессии
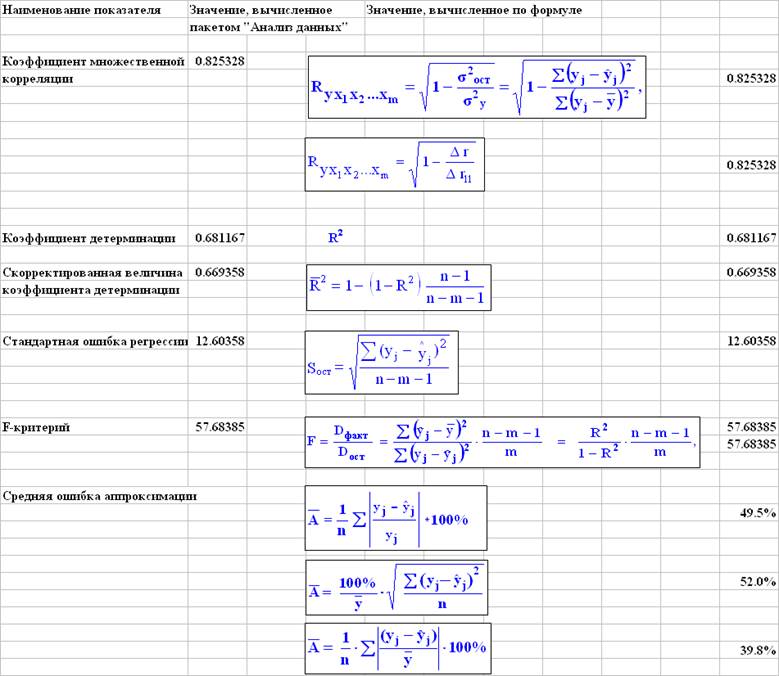
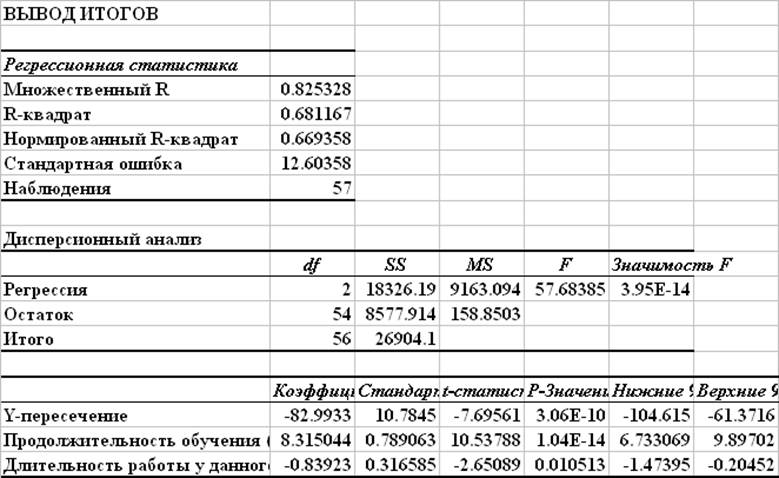
В результате построения модели множественной регрессии с информативными факторами получено уравнение регрессии часового заработка y на продолжительность обучения x2 и стаж работы у данного работодателя x4:.
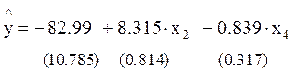
В скобках указаны стандартные ошибки параметров регрессии.
Недостаточно высокая величина коэффициента детерминации (0.67 < 0.8) и высокое значение средней ошибки аппроксимации (более 15%) ограничивают область возможного применения полученной модели.
Построение уравнения множественной регрессии с помощью пакета STATISTICA
Построение модели методом исключения
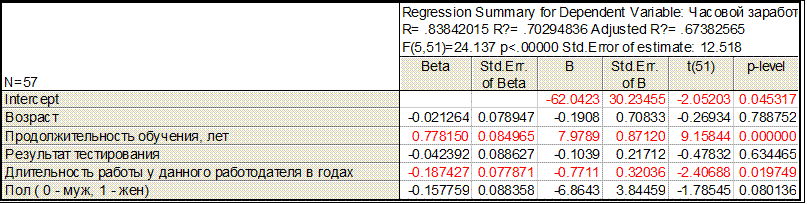
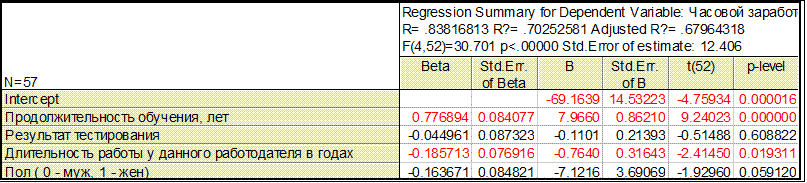
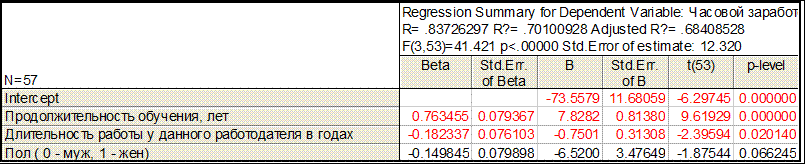

Построение модели методом включения


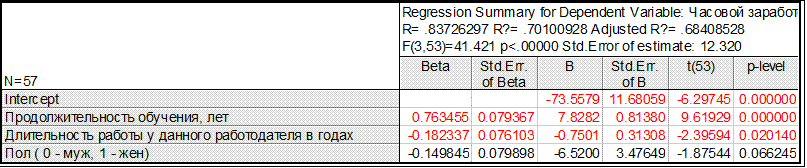
Результаты применения методов исключения (backward stepwise) и включения (forward stepwise) для построения модели регрессии с информативными факторами полностью соответствуют полученным ранее с помощью пакета "Анализ данных".
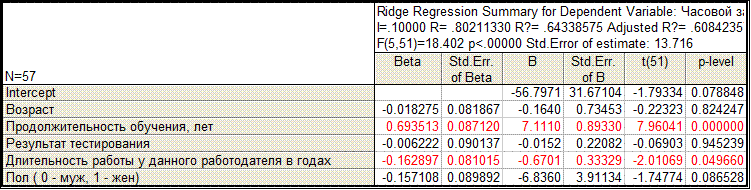
Построение модели методом ридж-регрессии для разных значений l
l=0
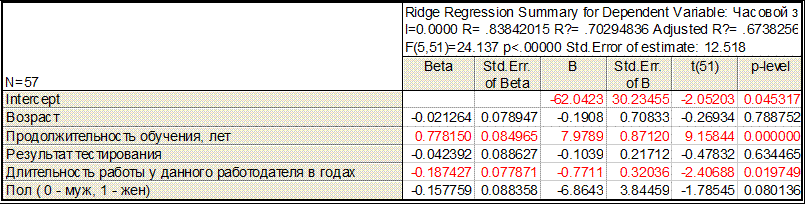
l=0,1
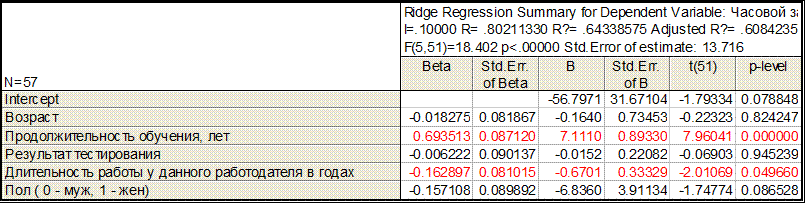
l=0,2

l=0,3
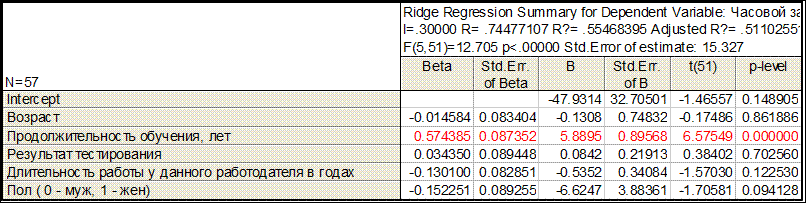
l=0,4

Зависимость характеристик точности модели от параметра l
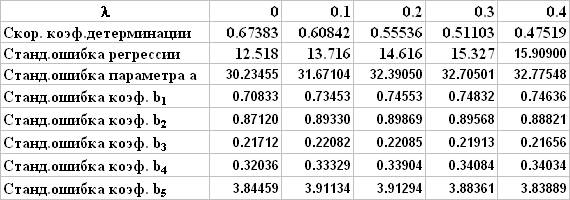
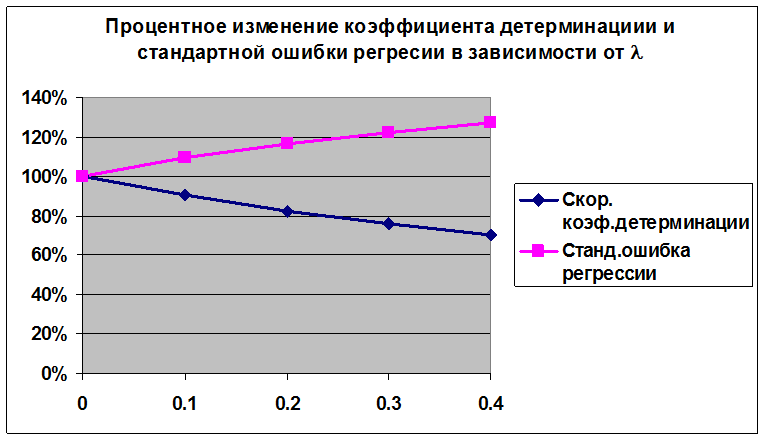
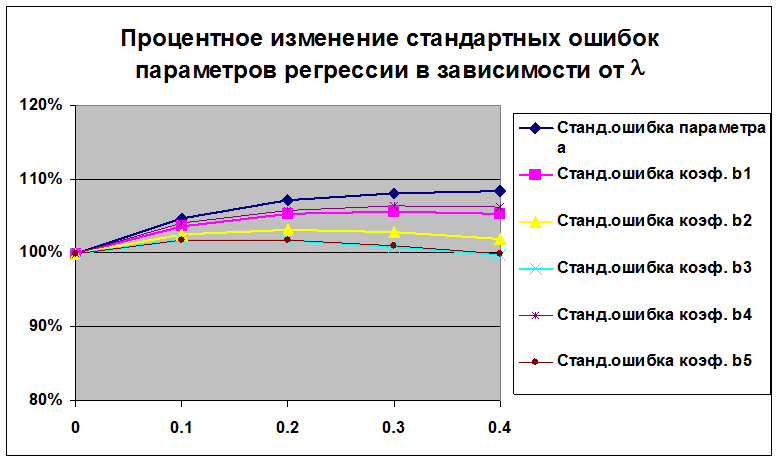
При увеличении l уменьшается коэффициент детерминации, увеличивается стандартная ошибка регрессии, увеличиваются стандартные ошибки параметров регрессии. Неблагоприятное изменение показателей качества модели при использовании ридж-регрессии объясняется низкой степенью мультиколлинеарности факторов. Для данного примера подходящим значением l следует считать 0.
Матричные вычисления ридж-регрессии для стандартизованной модели
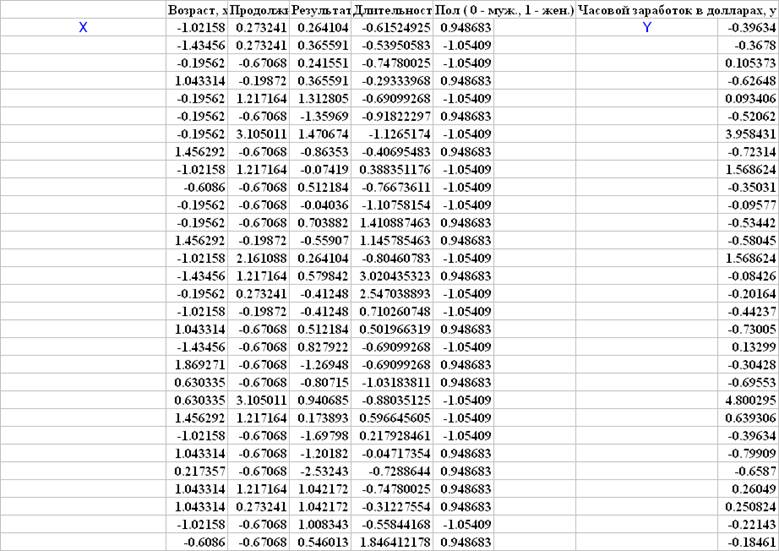
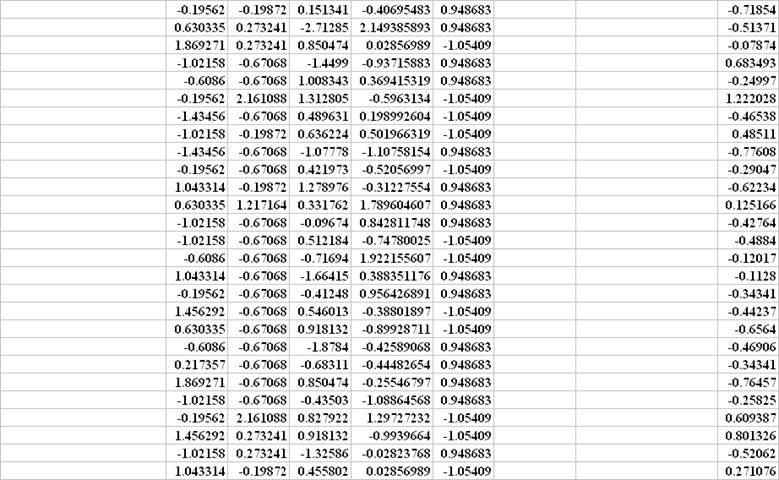
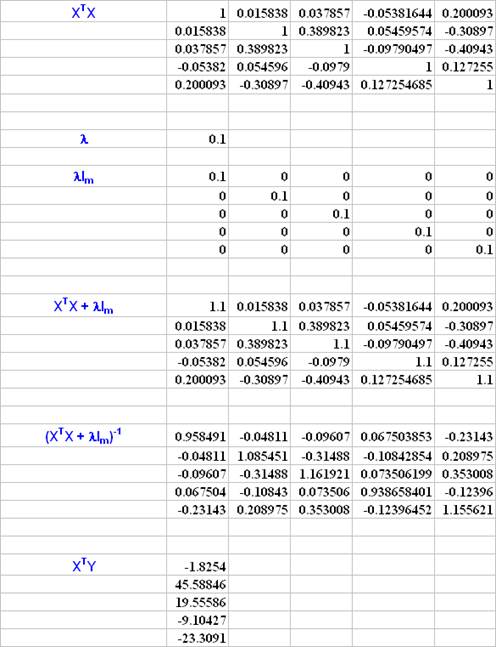

Полученные на основе матричных вычислений параметры модели ридж-регрессии совпадают с результатами применения пакета STATISTICA.
Расчет точечного прогноза результативного показателя и доверительного интервала прогноза
Матричные вычисления
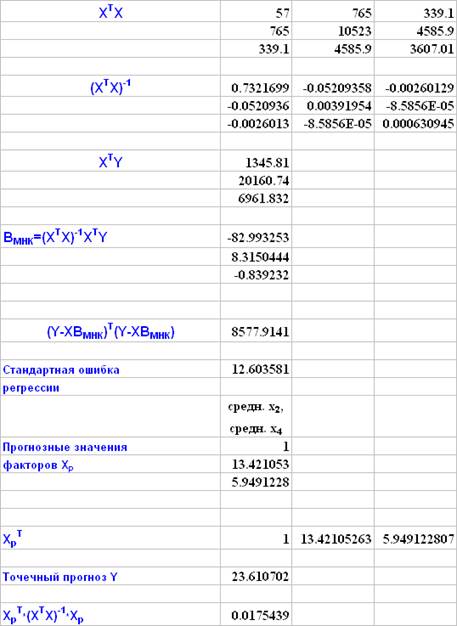
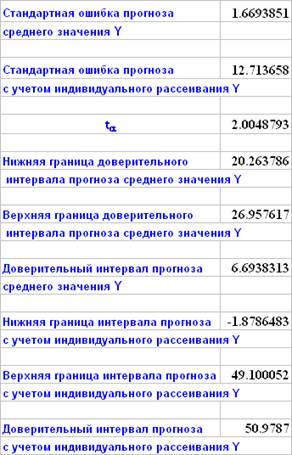
Использование пакета STATISTICA
Границы доверительного интервала прогноза среднего значения y:

Границы доверительного интервала прогноза y с учетом индивидуального рассеивания:

Зависимость доверительных интервалов прогноза от прогнозных значений факторов
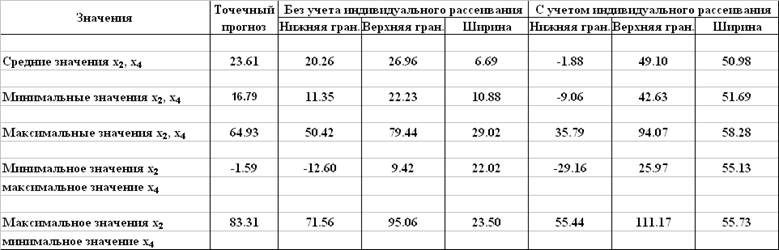
Ширина доверительного интервала точечного прогноза результативного показателя (часового заработка) минимальна для средних значений факторов и равна 6,69 долларов (28,4% от точечного прогноза). За счет индивидуального рассеивания результативного показателя ширина доверительного интервала увеличивается при средних значениях факторов более чем в 7 раз. При прогнозных значениях факторов, близких к граничным выборочным значениям, ширина доверительных интервалов точечного прогноза возрастает в 1.6 ¸ 4.3 раза, при этом имеет место сближение доверительных интервалов точечного прогноза и прогноза с учетом индивидуального рассеивания результативного показателя.
Наличие отрицательных значений нижних границ доверитльных интервалов, не имеющих экономического смысла, свидетельствует о недостаточной точности модели. Ее можно рекомендовать лишь для прогнозирования средних значений часового заработка при прогнозных значениях фактора x4 (длительность работы у данного работодателя), не превышающих 8 лет.
Анализ остатков
Графики остатков
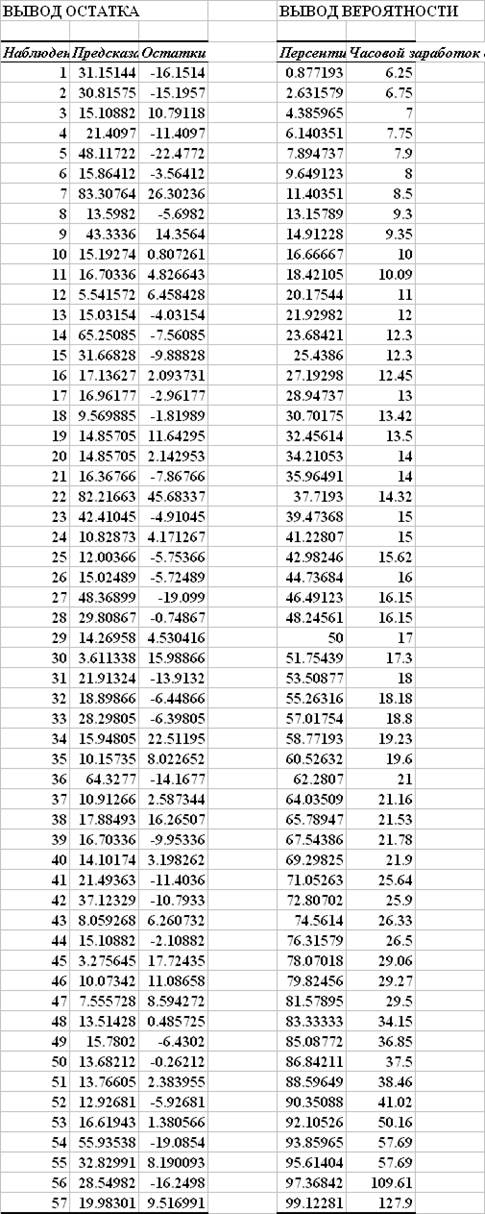
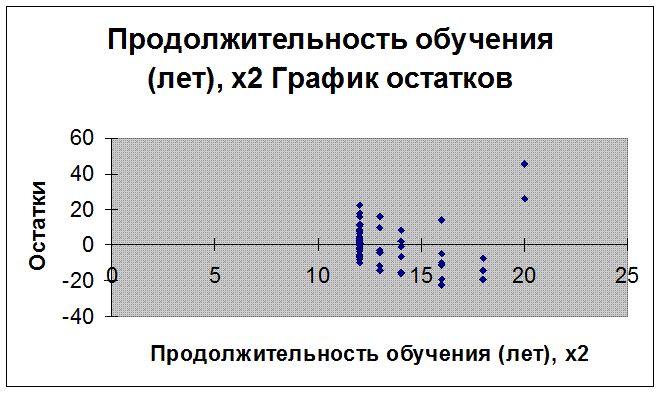
Визуальный анализ графика остатков по фактору x2 (продолжительность обучения) не дает основания считать остатки гетероскедастичными.
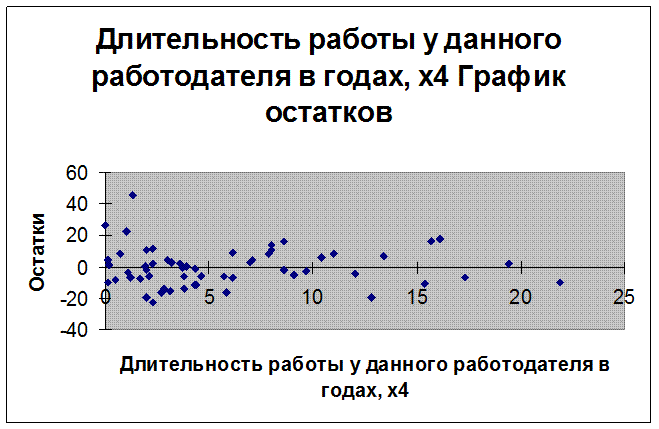
В графике остатков по фактору x4 (длительность работы у данного работодателя) прослеживается слабая тенденция к уменьшению дисперсии остатков с ростом x4.
График нормального распределения результативного показателя
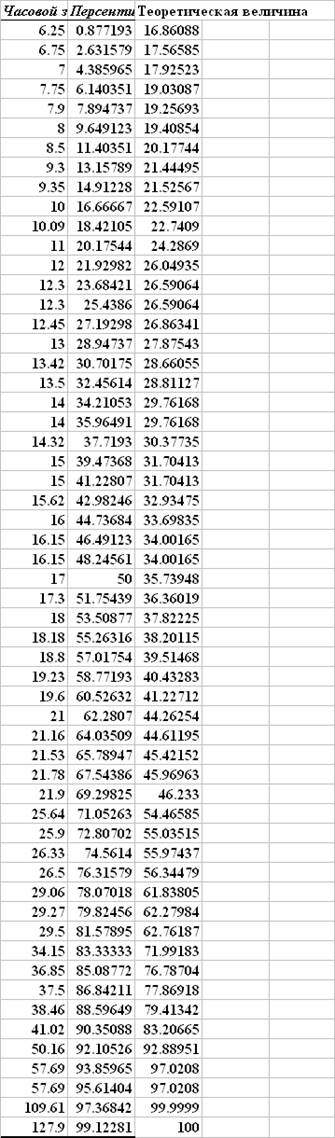
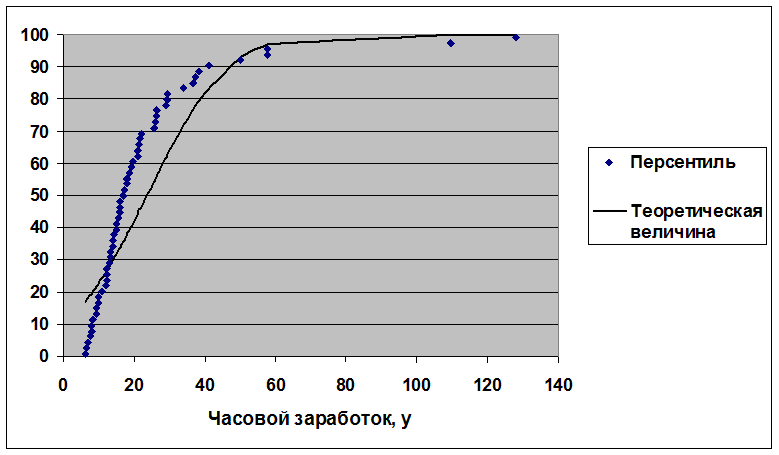
Характер выборочного распределения остатков соответствует нормальному закону, но расхождения между выборочными и теоретическими значениями достаточно велики. В данном случае на основе визуального анализа нельзя уверенно утверждать, что распределение остатков соответствует нормальному закону.
Тест Гольдфельда-Квандта
Проверка гомоскедастичности остатков по фактору x2 (продолжительность обучения)
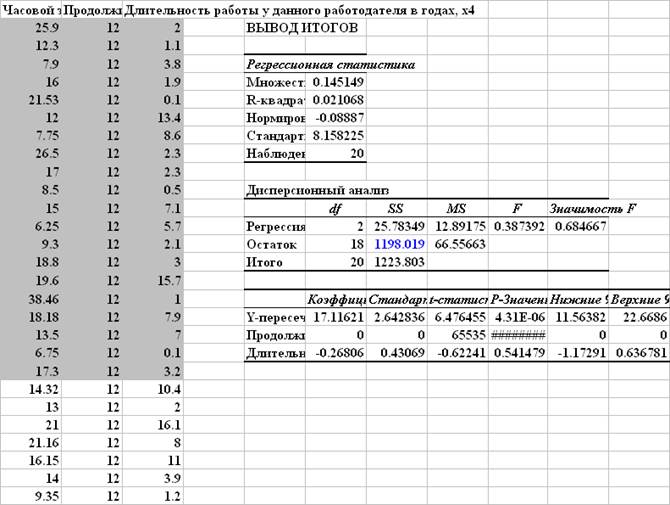
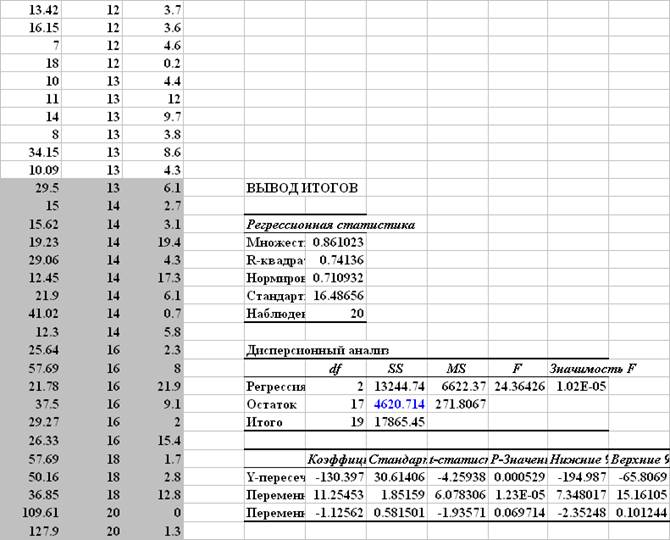
Расчетная величина F-критерия:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.