Исследование заданного механизма. Структурный анализ механизма. Схема заданного механизма

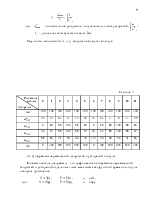
Поскольку в задании отсутствуют внешние активные моменты М_i формула (11) упрощается и принимает вид

M_пр  _ⁿ P ^vi cos_i ^_                                                               (12)

                                                                    i1 _ i _{1               }

где    P_i  - есть активные силы, Силы инерции звеньев не должны входить в число сил  P_i .

Составляем таблицу для будущего графика.

Используя данные кинематического анализа (лист №1), вычисляем величину углов _i для 12 положений механизма. Для этого на каждом из 12 планов скоростей отыскиваем точки, соответствующие местам приложения внешних сил, прикладываем в этих точках векторы внешних сил и измеряем угол между векторами P_i и v_i . Результаты заносим в таблицуM _пр  f .

Масштабы графика _ и  _м вычисляем по формулам:

                               м  My^пр,_max^max  ¹²⁸200  0,64  ^^нмм^{ м}    -  масштаб по оси ординат.

                                          _ 2l     1802 0.035    _рад_мм _    -  масштаб по оси абсцисс;

                                                    

Здесь:    M _пр,max - максимальное значение приведенного момента; y_max - отрезок (в мм), отражающий величину M _пр,max на графике. 

l  - отрезок (в мм) по оси  , соответствующий одному полному циклу механизма (один полный оборот кривошипа).

График работ сил сопротивления 

Если графически проинтегрировать кривую M _пр , получим график работ A_C  f  для рабочей машины. Для этого через точки 1, 2, 3, … на оси абсцисс графика M _пр  f  проводим вертикальные прямые. В результате получим трапеции с криволинейными верхними границами. Эти трапеции превращаем в равновеликие прямоугольники с высотой v_ср,1, v_ср,2 , … Вершины прямоугольников сносим на ось M _пр и из полюса Р, взятого на произвольном расстоянии Н, проводим в снесѐнные точки лучи Р1, Р2, Р3 …

Под графиком M _пр  f  проводим оси будущего графика A_C  f . От начала координат при помощи лучей Р1, Р2, Р3 … строим верѐвочную кривую, проводя отрезки 0-а,  a-b,  b-c …, параллельные лучам Р1, Р2, Р3 … Полученная ломаная линия представляет собой приближѐнный искомый график A_C  f . Масштаб полученного графика будет:

_A  _м _ H  0,64*0,35*60 13,44, где          _A - масштаб по оси работ;

_м - масштаб по оси приведенных моментов; рад

_ - масштаб по оси    в ; мм

Н – полюсное расстояние на графике приведенных моментов сил в мм.

Учитывая, что за цикл установившегося движения ^A_д  ^A_C, соединим прямой линией начало и конец полученной кривой A  f . Тогда получим график A_д  f  для рабочей машины.

Если теперь графически продифференцировать полученный график прямой линии, то получим зависимость M_д  f . Для этого из полюса Р проводим прямую, параллельную графику прямой линии до пересечения еѐ с осью M _пр , а затем из полученной точки проводим линию, параллельную оси абсцисс. Это и будет искомый график.

График избыточной работы

Эту зависимость получаем, вычитая из ординат графика A_д  f  ординаты графика AC  f  для каждого положения механизма:   Aизб  Aд  АC . Соединив полученные точки плавной кривой, получаем требуемый график A_изб  f .

Диаграмма энергомасс

График зависимости A_изб  f J _пр  получаем путѐм графического исключения параметра  из графиков J _пр  f  и A_изб  f . Для этого через одноимѐнные точки этих кривых проводим соответственно вертикальные и горизонтальные прямые, на пересечении которых получаем точки искомого графика A_изб  f J _пр .

Проведя через эти точки плавную замкнутую кривую, получаем диаграмму энергомасс A_изб  f J _пр . После построения этой кривой вычисляем углы наклона касательных к диаграмме энергомасс, соответствующие максимальной и минимальной угловой скорости ведущего звена внутри одного полного цикла установившегося движения.

                                                                   tg^max  ^J          _ср² 1_ ^1,7*104 *50² (1 0,17)  0,0195;                         

                                                                                        2_A                                       2*13,44

tg_min  ^J ср² 1 ^{1,7*104 2} (10,17)  0,013. *50

                                                                                        2_A                                       2*13,44

Где  _max и  _min - максимальный и минимальный угол наклона касательной;

2

 _J - масштаб графика приведенного момента инерции механизма ^кгм ; мм

 _A - масштаб графика работ, ^дж ; мм

рад

_ср - средняя скорость звена приведения, ; с

  - заданный коэффициент неравномерности движения механизма.

По вычисленным значениям тангенсов находим углы _max и  _min в градусах и проводим касательные под этими углами к диаграмме энергомасс соответственно в верхней и нижней части. Отрезок (ab) на оси ординат, отсечѐнный этими касательными, соответствует наибольшему изменению кинетической энергии маховика в течение одного цикла установившегося движения механизма.

Требуемый приведенный момент инерции маховика вычисляем по формуле

(13)     где     J _пр,м  - приведенный момент инерции маховика [кгм²];

(ab) -  отрезок в мм, отсекаемый касательными на оси ординат диаграммы энергомасс;

 _A - масштаб графика работ, ^дж ;

мм

рад

_ср - средняя скорость звена приведения, ; с

  - коэффициент неравномерности движения механизма.

Определяем размеры маховика. Наиболее удобной формой маховика является форма  диска с тяжѐлым  ободом. Влиянием спиц и втулки обычно пренебрегают. Тогда момент инерции J_м маховика равен:   

² mD²                                                    (14)

J_м mR 

4  Обычно задаются соотношениями размеров для обода маховика:                   h 0.1D,       b 1.5h  0.15D.

Приняв эти соотношения, получаем формулу для диаметра маховика:

5  4J^м  84.9J^м                   5 84,9*2,58

                                                         D _{                   } 5                           _{                      } 0,489                                                 

                                                                       0.0471                         7800

(15) где  плотность материала маховика:

7800 кг/м³  - для стальных;     7200 кг/м³ - для чугунных маховиков