Расчет электрических цепей при импульсном воздействии. Спектральная плотность входного и выходного сигналов

Министерство информационных технологий и связи РФ

СибГУТИ

Кафедра ТЭЦ

Курсовая работа

По курсу ОТЦ

Тема: Расчет электрических цепей при импульсном воздействии

Выполнил:

                                                        Проверила:

Новосибирск 2005

Рецензия.
Содержание.

СТР.

Рецензия.Содержание. 1

Содержание. 2

Введение. 3

1. Техническое задание. 4

2. Расчет цепи. 5

3. Интеграл Дюамеля. 7

4. Спектральная плотность входного и выходного сигналов. 9

5. Передаточная характеристика цепи. 11

6. Спектральная плотность входящего и выходящего сигналов. 12

6. Импульсная характеристика. 13

7. Дискретизация. 15

9. Z-преобразования импульсной характеристики цепи. 17

10. Z-преобразование импульсной характеристики корректора. 18

Заключение. 20

Список литературы. 21

Введение.

Цель курсовой работы состоит в систематизации и закреплении знаний, полученных студентами при изучении классического, операторного и спектрального метода расчёта процессов в линейных электрических цепях, а также теоретических основ анализа дискретных сигналов и линейных дискретных систем.

Было проведено моделирование просто реализуемого метода нелинейного восстановления сигнала. В результате работы я научился использовать основные методы восстановления сигнала.

1. Техническое задание.

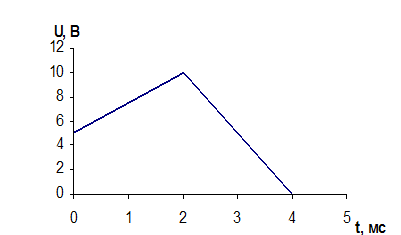
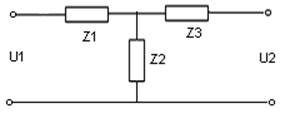
Задание на курсовую работу содержит схему анализируемой цепи и входной сигнал в виде ограниченного импульса.

            

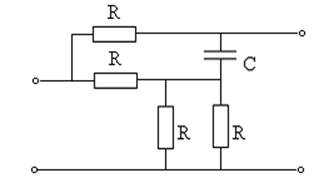
Все резисторы схемы имеют сопротивление R=1кОм, индуктивность катушки C=1мкФ.

В процессе выполнения необходимо получить следующие результаты:

2.1 рассчитать и построить график напряжения на выходе цепи U_вых(t);

2.2 вычислить и построить функцию цепи H(jw), спектральную плотность сигнала на входе и выходе цепи, построить соответствующие графики;

2.3 используя импульсную характеристику цепи, получить выражение для передаточной функции;

2.4 провести дискретизацию входного сигнала и импульсной характеристики цепи, вычислить  отсчёты дискретного сигнала на выходе и построить графики спектра дискретизированного сигнала и АЧХ дискретизированной цепи;

2.5 по отсчётам входного сигнала вычислить его спектральную плотность;

2.6 составить схему дискретной цепи, выполнив Z – преобразования дискретизированной импульсной характеристики;

2.7 определить передаточную функцию цепи, корректирующей искажения дискретного сигнала, вносимые сконструированной дискретной цепью, рассчитать дискретный сигнал на выходе корректора.

2. Расчет цепи

Интеграл Дюамеля может быть получен, если аппроксимировать приложенное воздействие f1(t) с помощью единичных функций, сдвинутых относительно друг друга на время ∆.

Вторая форма интеграл  Дюамеля может быть получена с помощью теоремы свертки.

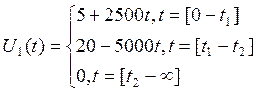
Uпр (С-«ХХ»)

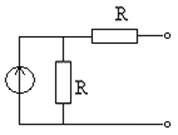
Uпр=1

U(0) (C – «КЗ»)

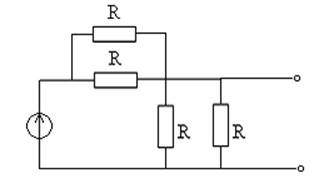
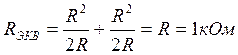
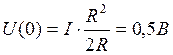
Для нахождения р преобразуем схему

3. Интеграл Дюамеля

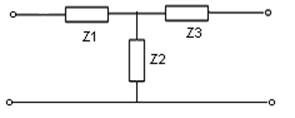
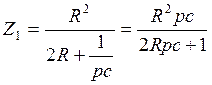
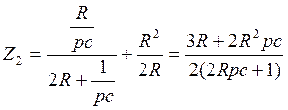
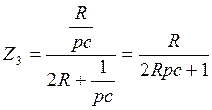
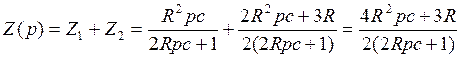
Исходный сигнал:

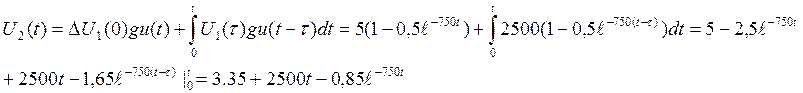
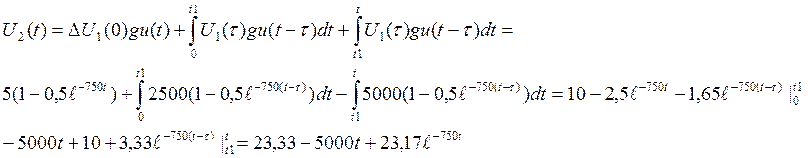
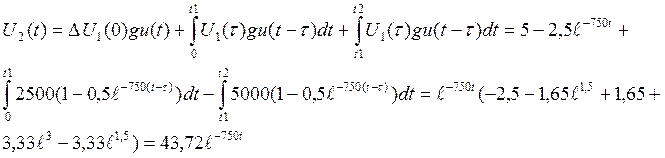
Значения U2(t), вычисленные с помощью интеграла Дюамеля.

t,мс	0	0,2	0,4	0,6	0,8	1	1,2	1,4	1,6	1,8	t1-	t1+	2.2
U2,В	2,5	3,11	3,71	4,29	4,85	5,41	5,95	6,48	7,01	7,53	8,05	8,05	7,79
t,мс	2,4	2,6	2,8	3	3,2	3,4	3,6	3,8	t2-	t2+	4,5	5	6
U2,В	7,43	7	6,48	5,9	5,28	4,6	3,88	3,13	2,35	2,35	1,62	1,11	0,53

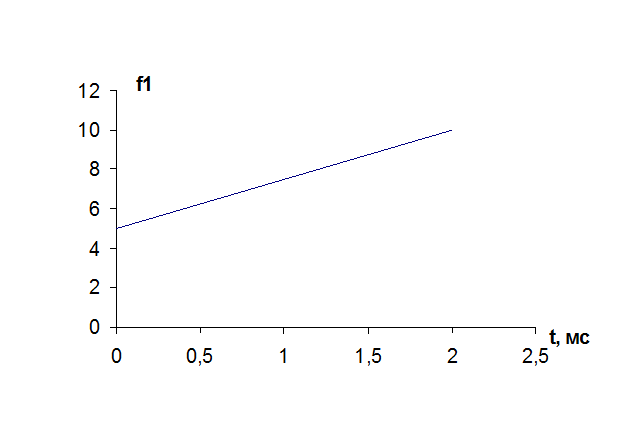
Зависимость входного сигнала от времени.

4. Спектральная плотность входного и выходного сигналов.

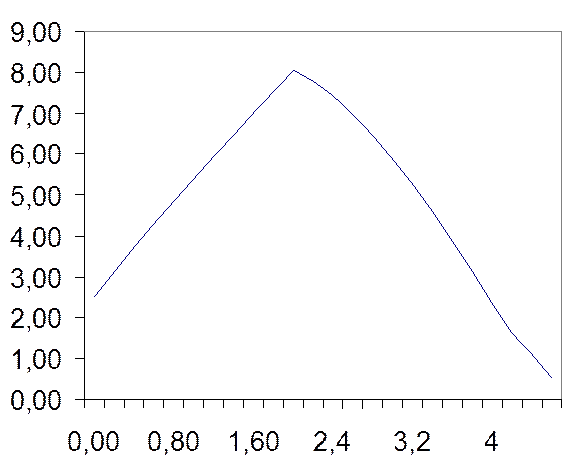
Рассмотрим входной сигнал как сумму «простейших» функций:

5. Передаточная характеристика цепи.

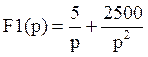
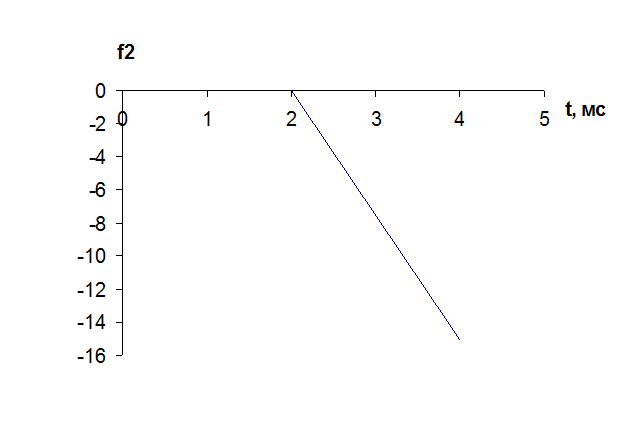
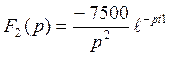
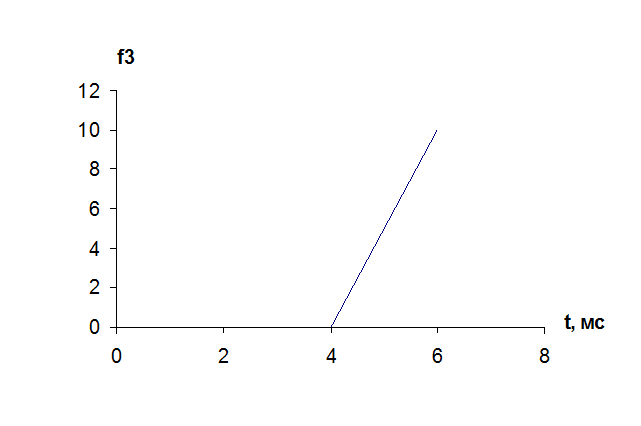
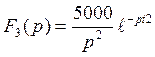
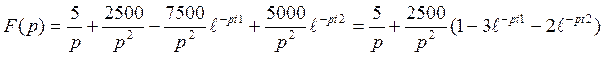
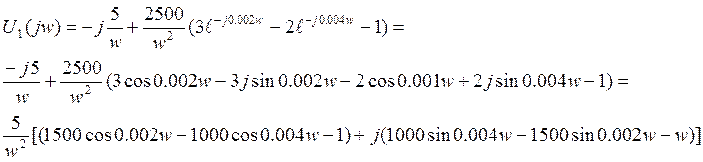
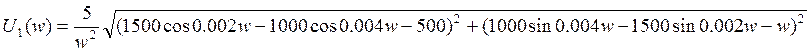
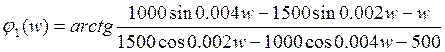
Передаточная характеристика цепи – это отношение изображения выходной реакции цепи к изображению входного воздействия.

Используем преобразованную схему, заменяя  p  на  jw.  

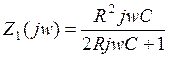
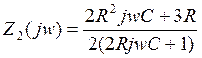
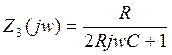
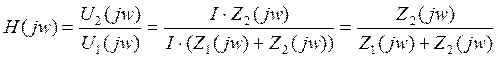
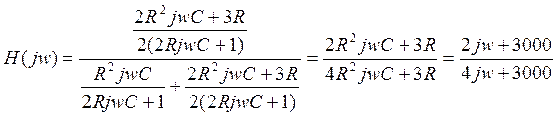
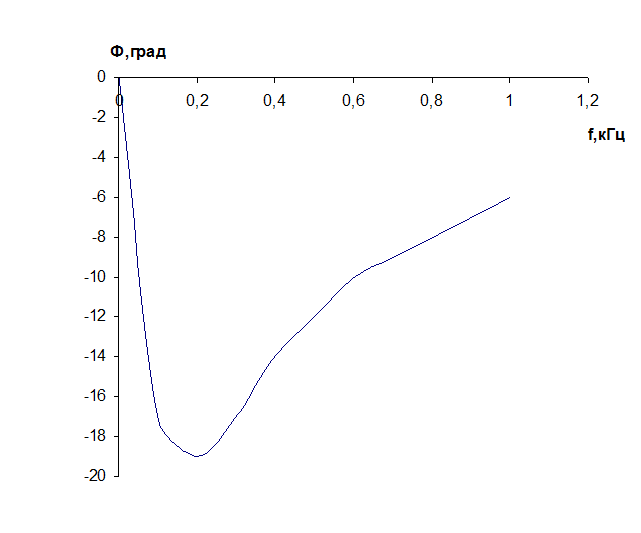
АЧХ: 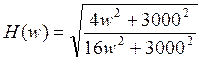      ФЧХ:  

6. Спектральная плотность входящего и выходящего сигналов.

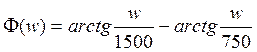
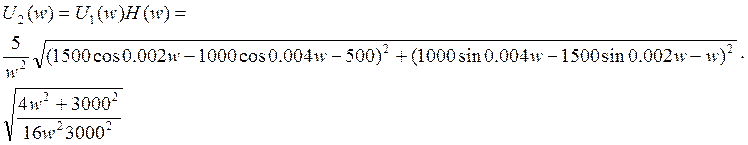
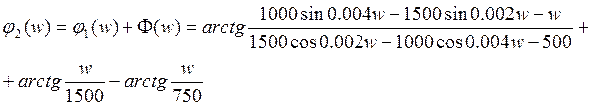
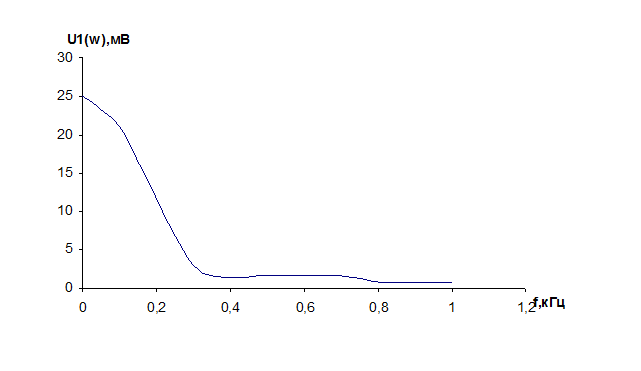
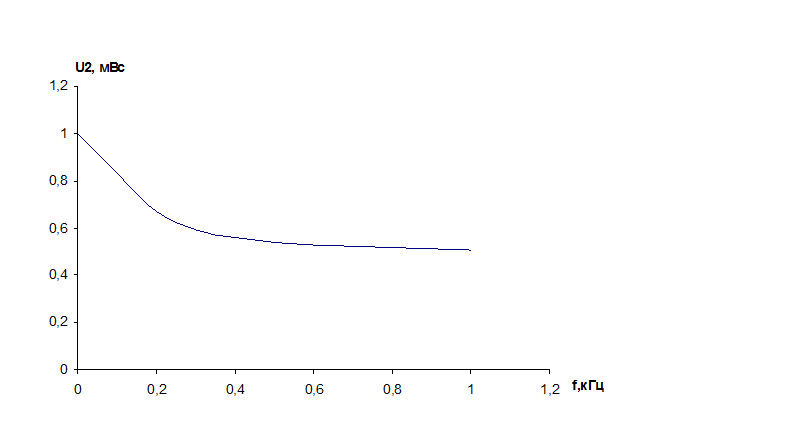
Частотные характеристики цепи и сигналов.

f, кГц	U1,мВ*с	1,град	Н	Ф,град	U2,мВ*с	2,град
0	25	0	1	0	25	0
0,1	21	62	0,831	-17	17,5	45
0,2	11,7	123	0,669	-19	7,8	104
0,3	2,86	178	0,594	-17	1,7	162
0,4	1,46	65	0,558	-14	0,81	51
0,5	1,59	90	0,539	-12	0,86	78
0,6	1,64	80	0,528	-10	0,87	70
0,7	1,7	108	0,521	-9	0,88	99
0,8	0,75	122	0,516	-8	0,39	114
0,9	0,76	81	0,513	-7	0,39	74
1	0,8	90	0,51	-6	0,41	83

6. Импульсная характеристика

hu(t)=gu(0)δ(t)+gu’(t)=0.5δ(t)+375e^-750t

7. Дискретизация

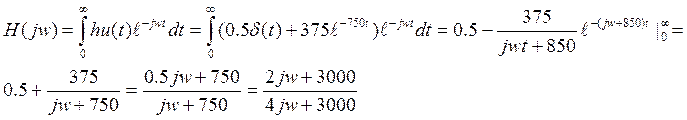
Дискретные значения функции входного сигнала и импульсные характеристики.

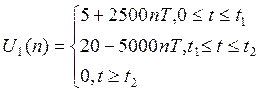
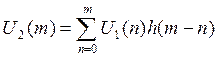     fg=2fв=2кГц      Т=0,2 нс

n	0	1	2	3	4	5	6	7	8	9	10
t,мс	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
U1,B	2.5	5.5	6	6.5	7	7.5	8	8.5	9	9.5	10
H	0.57	0.06	0.056	0.048	0.041	0.035	0.03	0.026	0.023	0.019	0.017
U2,B	1.43	3.28	3.78	4.32	4.94	5.56	6.02	6.61	7.15	7.64	8.13
n	11	12	13	14	15	16	17	18	19	20	21
t,мс	2.2	2.4	2.6	2.8	3	3.2	3.4	3.6	3.8	4	4.2
U1,B	9	8	7	6	5	4	3	2	1	0	0
H	0.014	0.012	0.011	0.009	0.008	0.007	0.006	0.005	0.004	0.003	0.002
U2,B	8.02	7.54	7.18	6.62	6.08	5.41	4.71	3.98	3.16	2.41	2.13

U₂(0)=U₁(0)*h(o)=2.5*0.57=3.28

U₂(1)=U₁(0)*h(1)+U₁(1)*h(0)=5.5*.057+2.5*0.06=3.28

U₂(2)=U₁(0*h(2)+U₁(1)*h(1)+U₁(2)*h(0)=3.78

Спектральная плотность дискретизированного сигнала U1(n)

9. Z-преобразования импульсной характеристики цепи

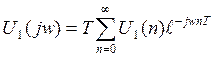
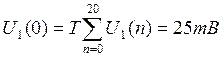
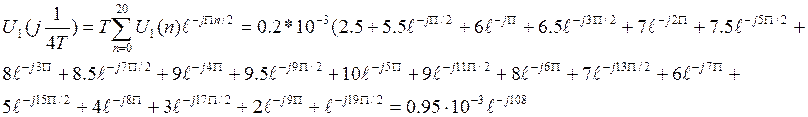
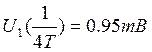
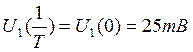
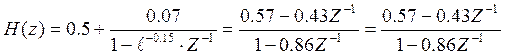
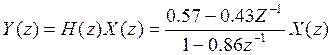
Схема дискретной цепи

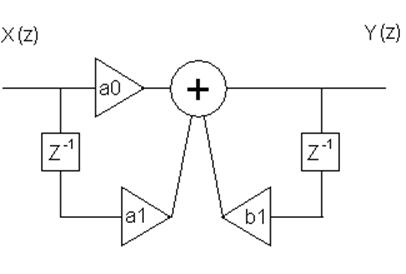
а₀=0,57

а₁=-0,43

b₁=0,86

Канонический вид схемы

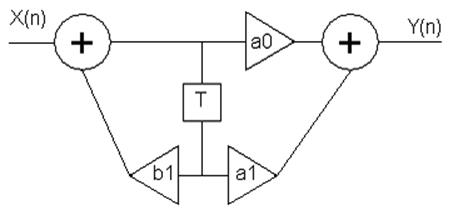
а₀=0,57

а₁=-0,43

b₁=0,86

y(n)=0.57x(n)-x(n)-0.43x(n-1)+0.86y(n-1)

10. Z-преобразование импульсной характеристики корректора

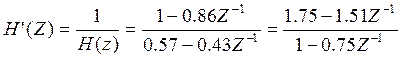
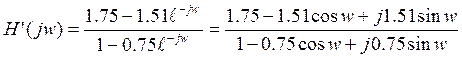
АЧХ корректора

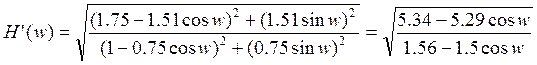
ФЧХ корректора

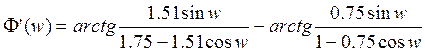
Получим отсчеты   hu’(n)

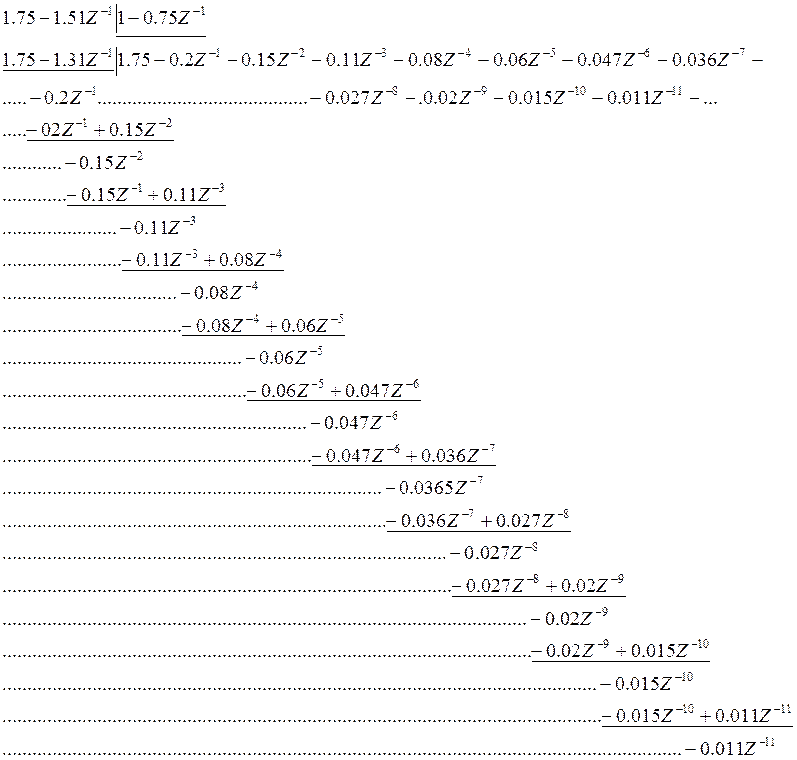
Дискретные отсчеты на выходе корректора

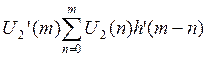
n	0	1	2	3	4	5	6	7	8	9	10
t,mc	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
h’	-0.2	-0.15	-0.11	-0.8	-0.06	-0.047	-0.036	-0.027	-0.02	-0.015	-0.011
U2,B	2.5	5.45	6.03	6.25	7.1	7.5	8.13	8.6	8.98	9.47	10.02
n	11	12	13	14	15	16	17	18	29	20	21
t,mc	2.2	2.4	2.6	2.8	3	3.2	3.4	3.6	3.8	4	4.2
h’	0	0	0	0	0	0	0	0	0	0	0
U2,B	9.08	8.03	6.94	5.9	5.01	3.97	2.87	1.96	1.04	0.02	0

Заключение.

Входе курсовой работы я провел анализ линейно-электрической цепи  во временной и частотной областях. Этот анализ заключался в переходной характеристике по напряжению и подсчета с ее помощью интеграла Дюамеля. При помощи программы DML я получил графическое изображение реакции цепи на сложное воздействие. Далее высчитали аналитические выражения для АЧХ и ФЧХ цепи, спектральных плотностей входного и выходного сигналов, а так же получили их графическое изображение при помощи программы FREAN. Чтобы проверить связь между временными и частотными характеристиками я применил формулу преобразования Фурье, при этом результат вычисления совпал с формулой Н(jw) полученной при нахождении передаточной функции цепи. Воспользовавшись теоремой Котельникова, определил частоту и период дискретизации входного сигнала. Затем при помощи теоремы свертки определил дискретный сигнал на выходе цепи. Далее используя аналогию между Z – преобразованием и преобразованием Фурье вычислил значения спектрально плотности входного дискретного сигнала на четырех частотах. При этом результат расчета практически совпал с результатами спектральной плотности аналогового сигнала. Получив выражение для Z – преобразования импульсной характеристике цепи, в соответствии с ней построил схему дискретной цепи и построил каноническую схему. Для компенсации искажений я составил схему корректирующей цепи