Расчет электрических цепей при импульсном воздействии. Расчет напряжения на выходе цепи. Переходная характеристика

Полученный график похож на спектральную плотность входного сигнала полученную в разделе 3.

 

7. Z – преобразование импульсной характеристики цепи

Преобразование импульсной характеристики цепи записывается в виде

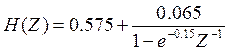
Учитывая, что Z- преобразование входного и выходного дискретных сигналов связанны между собой  соотношением:

                                                                                 

можем записать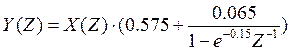

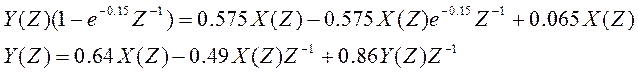
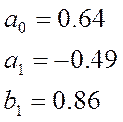
Схема дискретной цепи, реализующая это соотношение:

 

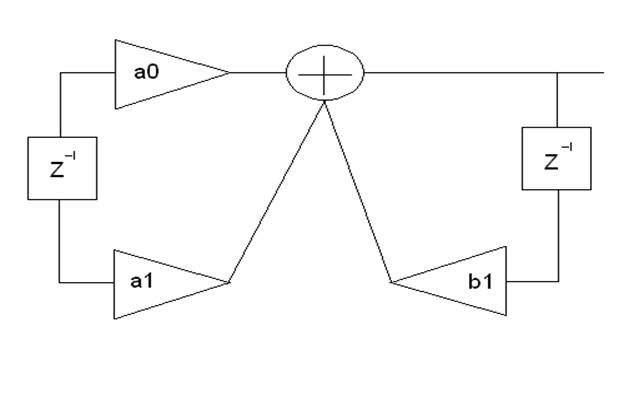
После приведения схемы к каноническому виду она примет вид:

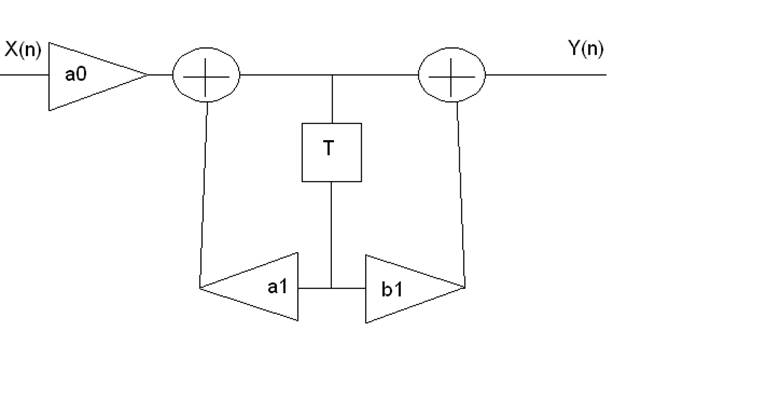
Коэффициенты передачи масштабных усилителей те же:

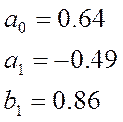
T - элемент памяти с задержкой на один период дискретизации. Коэффициенты передачи масштабных усилителей  те же, что и в предыдущей схеме.

Построю АЧХ дискретной цепи

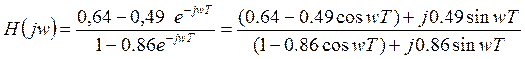
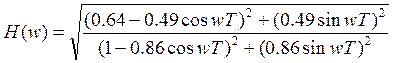
Таблица 7.1 – Значения АЧХ дискретной цепи

f,кГц	0	0.5	1	1.5	2	2.5	3	3.5	4	4.5	5
H	1.07	0.639	0.614	0.609	0.608	0.608	0.608	0.609	0.614	0.639	1.07

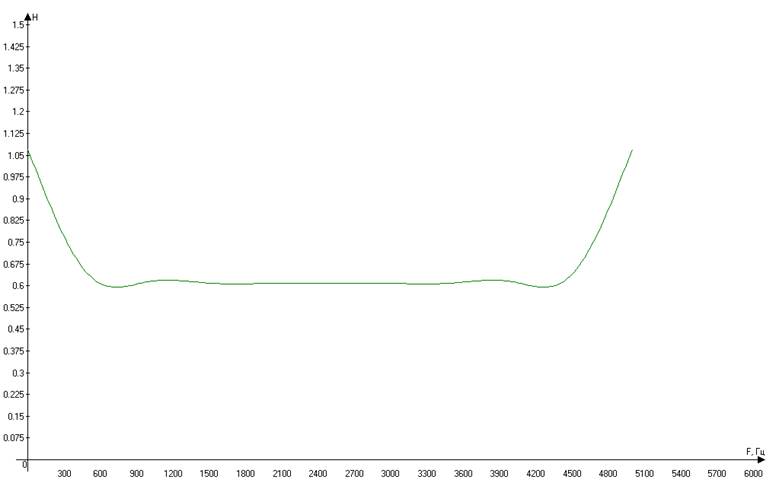
Рисунок 7.3 – АЧХ дискретной цепи

В этом разделе я определила Z-преобразование импульсной характеристики цепи и построила схему дискретной цепи реализующей его. Так же был построен график АЧХ цепи.

8. Расчет дискретного сигнала

                                      

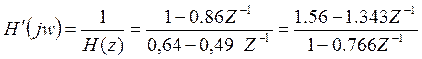
Отсчеты импульсной характеристики корректора находятся путем деления полинома числителя H’(Z) на его знаменатель и перехода от Z-преобразования к функции дискретного времени H’(n).

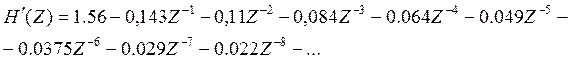
Дискретные значения сигнала на выходе корректора вычисляются с помощью формулы дискретной свертки.

                                                                              

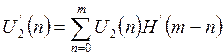
m=0

U₁(0)=U₂(0)H^I(0)=2.875*1.56=4.485

m=1

U₁(1)=U₂(0)H^I(1)+U₂(1)H^I(0)= 4.115

m=2

U₁(2)=U₂(0)H^I(2)+U₂(1)H^I(1)+U₂(2)H^I(0)=3.718

m=3

U₁(3)=U₂(0)H^I(3)+U₂(1)H^I(2)+U₂(2)H^I(1)+U₂(3)H^I(0)=3.301

m=4

U₁(4)=U₂(0)H^I(4)+ U₂(1)H^I(3)+U₂(2)H^I(2)+U₂(3)H^I(1) +U₂(4)H^I(0)=2.869

m=5

U₁(5)=U₂(0)H^I(5)+ U₂(1)H^I(4)+U₂(2)H^I(3)+U₂(3)H^I(2) +U₂(4)H^I(1)+

+U₂(5)H^I(0)=2.426

m=6

U₁(6)=U₂(0)H^I(6)+ U₂(1)H^I(5)+U₂(2)H^I(4)+U₂(3)H^I(3) +U₂(4)H^I(2)+

+U₂(5)H^I(1)+ U₂(6)H^I(0)=1.973

m=7

U₁(7)=U₂(0)H^I(7)+ U₂(1)H^I(6)+U₂(2)H^I(5)+U₂(3)H^I(4) +U₂(4)H^I(3)+

+U₂(5)H^I(2)+ U₂(6)H^I(1) +U₂(7)H^I(0) =1.514

m=8

U₁(8)=U₂(0)H^I(8)+ U₂(1)H^I(7)+U₂(2)H^I(6)+U₂(3)H^I(5) +U₂(4)H^I(4)+

+U₂(5)H^I(3)+ U₂(6)H^I(2) +U₂(7)H^I(1)+ U₂(8)H^I(0)=1.049

Таблица 8.1 -Дискретные значения импульсной характеристики корректора и сигнала на его выходе

Схема дискретной цепи, реализующая функцию корректора в соответствии с H’(Z) в канонической форме имеет вид, приведенный на расположенном рисунке, только значения коэффициентов масштабных усилителей примут значения а0=1,56 , а1=-1,34 , b1=0,766

Для того чтобы найти АЧХ корректора воспользуемся условием что:

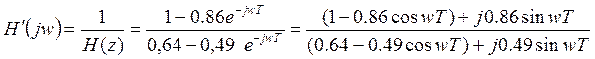
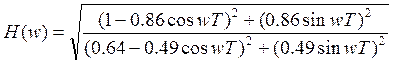
Таблица 8.1 – Значения АЧХ корректора                                                                 

f,кГц	0	0.5	1	1.5	2	2.5	3	3.5	4	4.5	5
H	0.93	1.564	1.628	1.641	1.645	1.646	1.645	1.641	1.628	1.564	0.93

Рисунок 8.1 – АЧХ корректора

В этом разделе я рассчитал дискретный корректор и построил его АЧХ. Определил схему реализующую корректор и определил элементы схемы.

 

Заключение

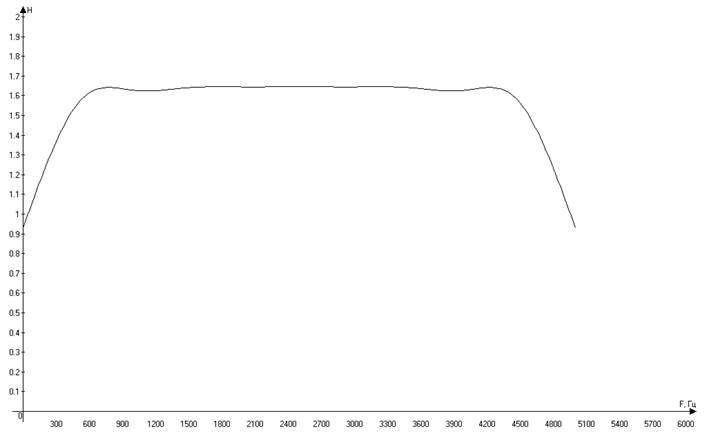
Входе выполнения курсовой работы я провела анализ линейно-электрической цепи  во временной и частотной областях. Этот анализ заключался в вычислении переходной характеристики по напряжению и подсчета с ее помощью интеграла Дюамеля. При помощи программы DML я получила графическое изображение реакции цепи на сложное воздействие. Далее высчитала аналитические выражения для АЧХ и ФЧХ цепи, спектральных плотностей входного и выходного сигналов, а так же получила их графическое изображение при помощи программы FREAN. Чтобы проверить связь между временными и частотными характеристиками я применила формулу преобразования Фурье, при этом результат вычисления совпал с формулой Н(jw) полученной при нахождении передаточной функции цепи. Воспользовавшись теоремой Котельникова, определила частоту и период дискретизации входного сигнала. Затем при помощи теоремы свертки определила дискретный сигнал на выходе цепи. Далее используя аналогию между Z – преобразованием и преобразованием Фурье вычислила значения спектральной плотности входного дискретного сигнала на четырех частотах. При этом результат расчета практически совпал с результатами спектральной плотности аналогового сигнала. Получив выражение для Z – преобразования импульсной характеристики цепи, в соответствии с ней построила схему дискретной цепи и привела ее к каноническому виду.

Эта курсовая работа помогла мне систематизировать знания полученные мною при изучении курса ОТЦ и подвела итог моим навыкам, полученным на практических и лабораторных занятиях.

Список используемой литературы

1.  Тихобаев В.Г. Расчет электрических цепей при импульсном воздействии - Новосибирск: