Анализ нагрузки. Выбор исполнительного двигателя. Расчет оптимального передаточного отношения редуктора, страница 3

Для того чтобы выбранные ПИП и собранный на их основе измеритель рассогласования удовлетворял заданной по ТЗ точности, нужно выполнить следующее условие:

, где 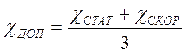, χ_СТАТ и χ_СКОР – из ТЗ.

Потенциометр выберем из следующих условий:

- мощность рассеивания потенциометра должна быть больше мощности, которая будет выделяться на нем при напряжении питания 27 В;

- угол активной зоны потенциометра должен быть больше максимального угла поворота нагрузки;

- выбранный потенциометр должен удовлетворять условиям точности.

Выберем для начала потенциометр ПЛП-11 со следующими параметрами:

Тип	ε, %	jр, рад	МТР·10-2, Н·м	R, Ом	Рр, Вт	м, кг
ПЛП-11	±0,3	5,76	0,705	500÷1000	2	0,048

Мощность, рассеиваемая на потенциометре:

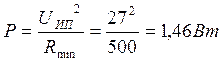 , что укладывается в допустимые пределы.

Угол активной зоны потенциометра намного больше требуемого; теперь проведем расчет точности.

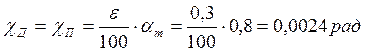, что соответствует 8´15´´,

, что соответствует 11´41´´,

.

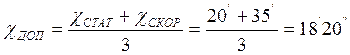Ошибка измерителя рассогласования меньше допустимой ошибки, определенной по техническому заданию, следовательно, выбранный потенциометр подходит.

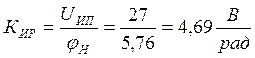
Можно провести расчет допустимой ошибки с учетом того, что нагрузкой является антенная установка:

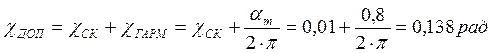, что соответствует 7⁰54¢.

Данная допустимая погрешность измерителя рассогласования получена из более мягких критериев, следовательно, потенциометр подойдет в любом случае.

На рис. 9 - принципиальная схема ИР, построенного по компенсационной схеме, на рис. 10 – внешний вид потенциометра ПЛП-11.

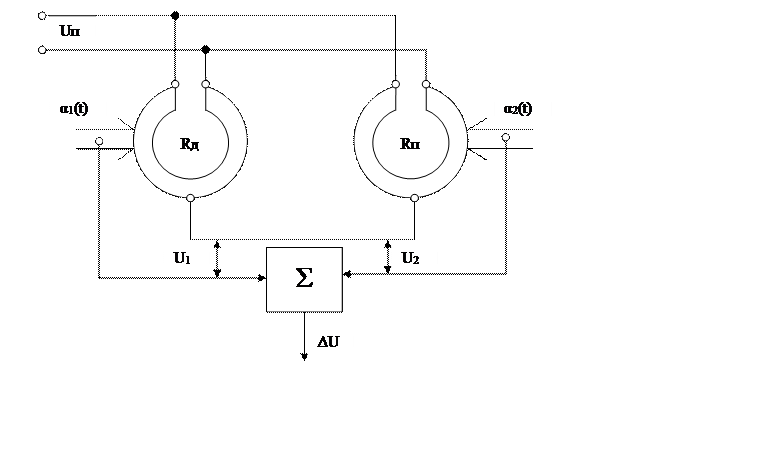
Рис. 9 Принципиальная схема ИР, построенного по компенсационной схеме

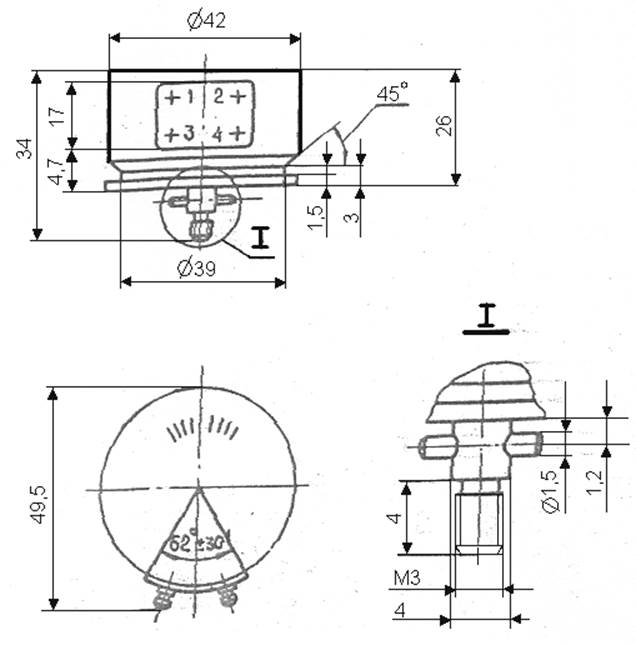
Рис. 10 Внешний вид потенциометра ПЛП-11

7.  Динамический расчет.

Для расчета системы на динамическую устойчивость нужно построить функциональную схему привода со всеми входящими в него параметрами. На рис. 11 приведена структурная схема привода антенны.

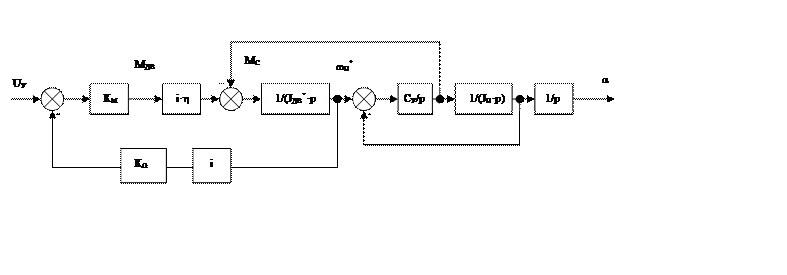
Рис. 11 Структурная схема привода антенны

Проведем расчет параметров, входящих в схему:

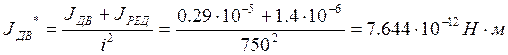
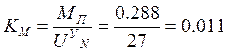
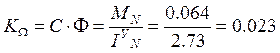
где С_У – коэффициент упругого скручивания (от 100 до 1000 Н·м/рад).

Если данную схему упростить, то получится другая структурная схема, приведенная на рис. 12.

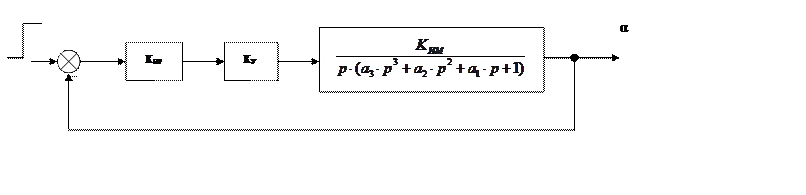
Рис. 12 Упрощенная структурная схема привода антенны

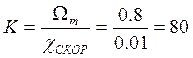
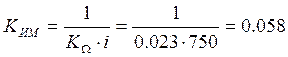
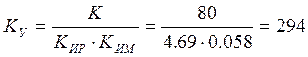
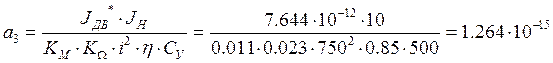
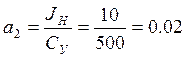
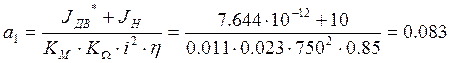
Для построения переходного процесса в программе MATLAB, подпрограмме Simulink, нужно построить схему, приведенную на рис. 13.

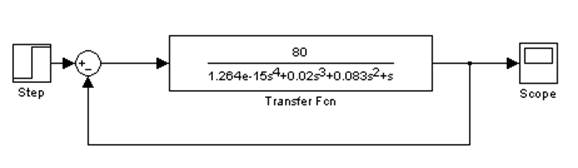
Рис. 13 Структурная схема в подпрограмме Simulink

Рассмотрим систему в малых отклонениях, которые можно считать линейными. Данная структура представляет собой математическую модель антенной установки. На входе системы – ступенчатая функция, которая представляет собой эквивалент поступления на вход сигнала управления на поворот на один радиан.

На рис. 14 и 15 приведены графики переходного процесса, представляющий собой резкое нарастание выходного сигнала.

Вывод: данная система неустойчива, для нормальной работы необходимо добавить корректирующее звено.

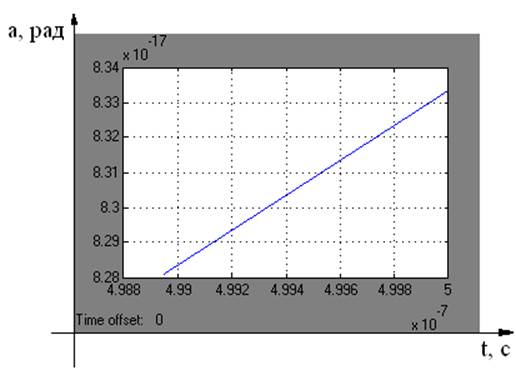
Рис. 14 График переходного процесса (влияние составляющей а₃ – быстрое нарастание сигнала в начальный момент времени)

К тому моменту, когда на переходный процесс начнут оказывать влияние коэффициенты а₂ и а₁ – процесс, обусловленный составляющей а₃, затухнет, и график будет иметь вид как на рис. 15.

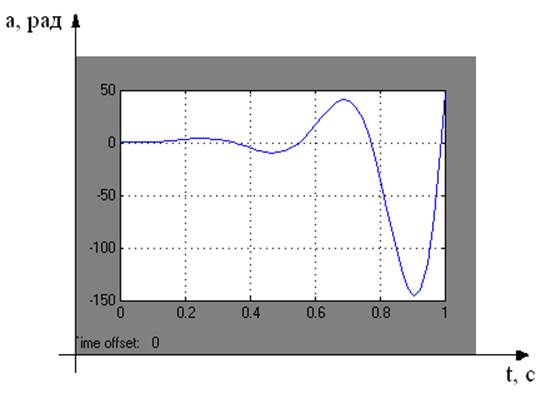
Рис. 15 График переходного процесса

Для построения корректирующего звена нужно представить передаточную функцию исходного звена в другом виде, при котором в знаменателе стоят элементарные сомножители.

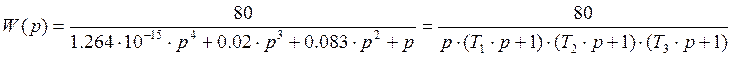
После решения знаменателя относительно p были найдены корни:

X₁=0;

X₂=-15822784810122.432278;

X₃=-2.075+i·6.76;

X₄=-2.075-i·6.76.

Теперь передаточную функцию можно записать в более удобном ви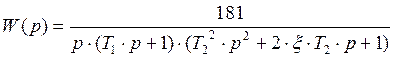де:

, где:

Т₁=6.32·10^-14, Т₂=0.141 с, ξ=0.294.

На рис. 16 построена логарифмическая амплитудная характеристика нескорректированной системы, на рис. 17 – логарифмическая фазовая характеристика.

Найдем параметры ω_к и А_к, которые позволят сформировать требования к низкочастотной части желаемой характеристики: чтобы ошибка воспроизведения гармонического сигнала не превышала заданную по техническому заданию, ЛАХ системы должна проходить выше минимум на 3дБ контрольной точки с координатами ω=ω_к, L(ω)=20lg(A_k/x_max).

,

,

.

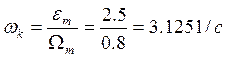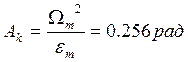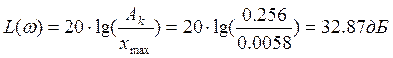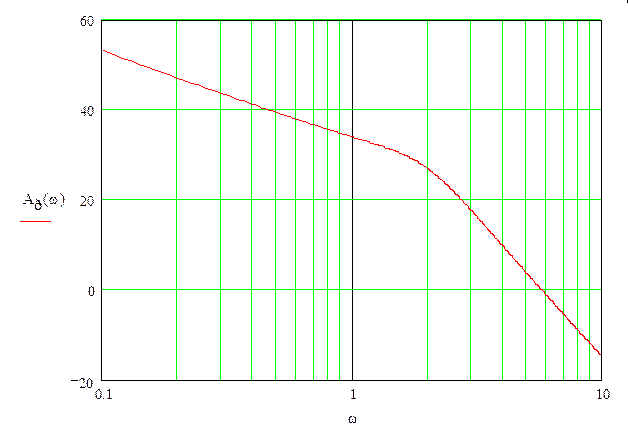
Рис. 16 ЛАХ нескорректированной передаточной функции

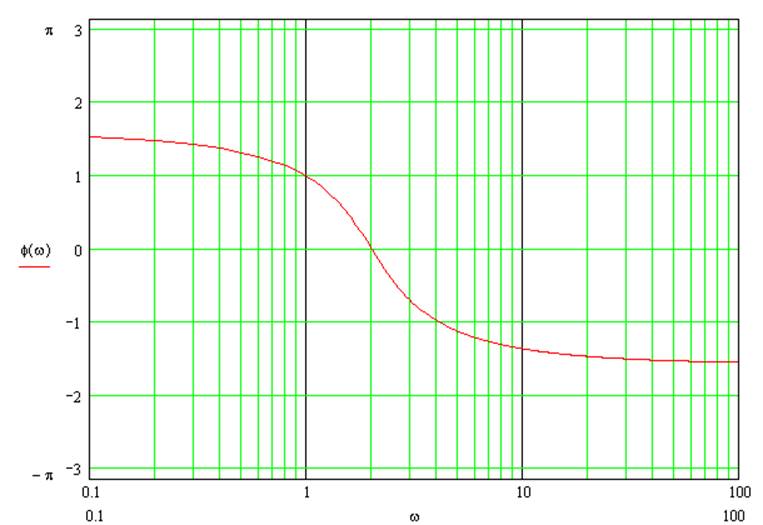
Рис. 17 ЛФХ нескорректированной передаточной функции

Как видно из графика, данная ЛАХ заходит в запретную зону, ограниченную точкой L(ω_к). Кроме того, пересечение оси абсцисс идет под наклоном -60дБ/дек и происходит это позже, чем график ЛФХ достигает значения -180⁰.