Определение оптимальной численности транспортных средств. Применение аналитического аппарата теории массового обслуживания и теории игр

4 Определение оптимальной численности

 транспортных средств

4.1. Применение аналитического аппарата теории массового обслуживания и теории игр

Теория массового обслуживания – это основанный на теории вероятности математический аппарат, исследующий вероятностные процессы и системы, связанные с образованием очередей.

Основной задачей массового обслуживания является установление зависимости между числом обслуживающих аппаратов и качеством обслуживания. Во всех системах массового обслуживания легко прослеживается вполне определенная структура, складывающаяся из ряда основных элементов:

1)  входящий поток требований, т.е. поток требований, нуждающихся в обслуживании и поступающих в обслуживающую систему;

2)  очередь;

3)  обслуживающее устройство, функционирование которого оценивают временем обслуживания;

4)  выходящий поток, т.е. поток требований покидающих систему обслуживания.

Применение теории массового обслуживания требует определенной схематизации исследуемого процесса и в первую очередь описания потока требований на обслуживание и времени обслуживания посредством некоторого закона.

В большинстве систем массового обслуживания (как и в рассматриваемой системе экскаватор - самосвалы) количество требований на облуживание, момент их поступлений и время обслуживания является случайными величинами, которые под влиянием случайных обстоятельств могут принимать различные значения. Такие системы массового обслуживания принято называть вероятностными.

Для полного описания входящего потока достаточно вычислить математическое ожидание числа требований, поступающих в систему обслуживания в единицу времени:

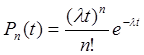                                   (4.1)

где Р_n(t)- вероятность того, что в момент времени t поступает n заявок на  обслуживание;

λ- параметр потока, т.е. математическое ожидание числа требований, поступивших в систему за единицу времени;

e – основание натуральных логарифмов.

Итак, с позиции теории массового обслуживания задачу можно описать следующим образом.

Система экскаватор – самосвалы при количестве последних, равном N, может находится К=N+1 состояния:

(К=0) – все N самосвалов в работе;

(К=1) – один самосвал простаивает, а (N-1)  работы;

(К=2) – два самосвала простаивают, а (N-2)  работы;

----------------------------------------------------------------------------------------------------------------------------------------------------------------(К=N) – все N самосвалов простаивают.

Каждое из этих состояний может быть задана следующей вероятностью;

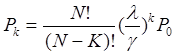                                                 (4.2)

Где N – количество самосвалов, находящихся в обращении

К – 0,1,2,…, N – возможные состояния системы;

Р₀ – вероятность того, что все самосвалы находятся в работе и не нуждаются в обслуживании

λ  среднее количество подходов самосвалов под погрузку в единицу времени;

γ- среднее количество самосвалов, загружаемых экскаватором в единицу времени.

На основании формулы можно определить можно определить простой экскаватора и каждого самосвала в процентах от продолжительности смены и различных количествах самосвалов:

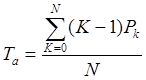                             (4.3)

В нашем дипломном проекте требуется определить оптимальное количество самосвалов МАЗ-503Б  грузоподъемность 7 тонн для работы с экскаватором ЭО-6112Б  с ковшом емкостью 1,25 м³.

Работа системы экскаватор - самосвалы характеризуется следующими условиями:

Дальность перемещения грунта L=2 км;

Среднее время погрузки одного самосвала t_п=3,9 мин =0,065 часа

Скорость передвижения самосвалов в грузовом и порожнем направлениях v=20 км/час;

Среднее время цикла обращения самосвалов

Т_ц=0,065+(2*2)/20+0,0217=0,287 часа.

Отсюда

λ=1/Т_ц=1/0,287= 4 рейсов/час, а интенсивность погрузки самосвалов экскаватором

γ=1/t_р=1/0,065= 15 машин/ч.

При дальнейшем расчете находим количество самоcвалов:

Т_ц/t_р=0,287/0,065=5 шт.

Учитывая, что интерес могут представлять состояния системы при количестве самосвалов, превышающем определённое, задаются несколько большим числом транспортных средств и подсчитывают при этом ожидаемые простои  экскаватора и транспортных средств.  

Для того чтобы в полной мере иметь возможность в полной мере судить о характере взаимодействия экскаватора и транспортных средств, необходимо оценить вероятность простоев в системе при разных количествах самосвалов.

Определим простои экскаватора и транспортных средств при количестве транспортных средств 7, 6, 4, 3.

Так как расчёты связаны с большим объёмом вычислений то были составлены специальные таблицы, значительно упрощающие расчёты.     

Как видно из формулы (4.2) , при данном количестве самосвалов вероятностный простой экскаватора и транспортных средств зависят только от соотношения  λ/γ= t_п/Т_ц.

               В рассматриваемом нами примере α= λ/γ=4/15=0,26. при количестве самосвалов, скажем, N=3 простой экскаватора Р₀=0,436, а простой одного самосвала – Т_с=0,270/3=0,090 и т.д.

Найденные таким образом ожидаемые простои экскаватора и самосвалов, в зависимости от количества последних представлены в таблице 4.1.

Таблица 4.1 -  Простои  экскаватора и самосвалов, в зависимости от количества последних