Числовые характеристики случайных величин. Основные законы распределения случайных величин

Понятие о начальных и центральных моментах случайных величин

Математическое ожидание и дисперсия являются частными случаями более общих числовых характеристик – моментов с.в. 

Начальным моментом порядка k случайной величины Х называется число ^ν_k , равное математическому ожиданию _X^k , таким образом, по определению  

 n

∑x p_i^k _i    − для дискретной с.в.

^ν_k = MX^k =                                                                      (6)

^ ∫ x f x dx^k ( ) − для непрерывной с.в.

−∞

Очевидно, что ν₁ = MX , т.е. математическое ожидание случайной величины Х является её начальным моментом первого порядка.

Центральным моментом порядка k случайной величины Х называется число ^µ_k , равное математическому ожиданию (X − MX)^k , таким образом, по определению

 n                        _k

_∑(x_i − MX) ⋅p_i      − для дискретной с.в.

^µ_k = M X( − MX) =                                                                    (7)

^ ∫           ^k ( )        − для непрерывной с.в.

(x − MX) f x dx

−∞

Очевидно, что

^_µ₁ = M X(    − MX) = MX − M MX(      ) = MX − MX = 0,                 ₂                                     (8) 

µ₂ = M X( − MX) = DX,

т.е. центральный момент первого порядка случайной величины Х равен нулю, а дисперсия  является центральным моментом второго порядка с.в. Х.

Из определений моментов, в частности, следует, что: ν₀ = µ₀ = 1

Модой M X₀ дискретной случайной величины Х называется её значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями. Для непрерывной с.в. мода M X₀ – точка локального максимума плотности вероятности f x( ).

Мода может иметь единственное значение (унимодальное распределение) или иметь множество значений (полимодальное распределение).

Медианой непрерывной с.в. называется действительное число

M X_e = x₀ ,                                                                  (9)                                              удовлетворяющее условию: P X( < x₀) = P X( > x₀) = ^{1 2}/ .  Таким образом медиана – это такое значение x₀ с.в. Х, для которого одинаково вероятно, окажется ли с.в. Х больше или меньше  x₀ . Для дискретных с.в. медиана обычно не определяется.

Пример 1. Задан ряд распределения дискретной случайной величины Х:

xi	-2	-1	0	1	2	3
pi	0.1	0.2	0.25	0.15	0.1	0.2

Найти MX, DX,^σ_X .

Решение. По формуле (1): 

MX =       ^{x p}_{i i} = −2 01 1 02 0 025 1 015 2 01 3 02 055⋅ . − ⋅ . +     ⋅ . + ⋅ .     +                                                    ⋅ . + ⋅ . = .  .

i=1

По формуле (4):

6

DX = ∑^{x p}_i² _i − (MX)² =MX = −( 2 01)² ⋅ . + −( 1 02 0 025 1 015)² ⋅ . + ² ⋅ .  + ² ⋅ .   + i=1    

+2 01 3 02 055² ⋅ . + ² ⋅ . − ( . )² = 26475.     .

По формуле (5): ^σ_X = 026475 1627.       = . .

Пример 2. Математическое ожидание и дисперсия с.в. Х равны соответственно  7/2 и   35/12. Найти математическое ожидание и дисперсию с.в. Y = 4X −1.

Решение. Используем свойства математического ожидания и дисперсии:

MY = M(4X −1) = M(4X) − M(1 4) =     ⋅ MX −1 4 7 2 1 13= ⋅( / ) − =        ,

²                                                                                                     

DY = D(4X −1) = D(4X) = 4 ⋅DX = 16 35 12 140 3⋅(      /          ) =     / .

Основные законы распределения случайных величин

• Биномиальный закон распределения.

Дискретная с.в. Х имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, ..., n с соответствующими вероятностями:

p_k = P X( = k) = C p q_n^{k k n k−} ,                                                 (1) где p − параметр распределения, 0 < p < 1,          q = 1− p, k = 0 1, ,...,n.  Случайная величина, распределенная по биномиальному закону,  равна количеству наступлений события А в nнезависимых опытах (числу «успехов» в схеме Бернулли), при условии, что вероятность наступления события А в каждом опыте одинакова и равна p. Ряд распределения с.в. Х имеет вид:

xk	0	1	2	⋅ ⋅ ⋅	k	⋅ ⋅ ⋅	n
pk	qn	C p qn1 1 n−1 = =npqn−1	C p qn2 2 n−2 = = n n( −1) p q2 n−2 2!	⋅ ⋅ ⋅	C p qnk k n k− = = n n( −1)... n( − +k 1) p qk n k− k!	⋅ ⋅ ⋅	pn

Можно доказать, что 

MX = np, DX = npq                                                                     (2)

Пример 1. Вероятность того, что изделие стандартно, равна 0.9. Проверяют 50 партий, в каждой из которых 5 изделий. Случайная величина Х – число партий, в каждой из которых 4 стандартных изделия. Найти MX, DX, ^σ_X .

Решение. Пусть событие А – в партии 4  стандартных изделия. Тогда

.в. Х распределена по биномиальному закону,

n = 50, p = P A( ) = 032805. . По формулам (2):

MX = np = 50 032805 164⋅ .                                       = . , DX = npq = 50 032805 1 032805 1102⋅ .            ⋅( − .                                        ) =       .                 ,

^σ_X =    DX = 332. .

Следовательно, среднее число партий, содержащих 4 стандартных изделия, приблизительно равно 16, а разброс относительно этого значения приблизительно равен трём.

• Распределение Пуассона.

Примерами дискретных с.в., имеющих распределение Пуассона, являются: количество вызовов на телефонной станции за время t ; число опечаток в большом тексте, число бракованных деталей в большой партии; число α-частиц, испускаемых радиоактивным источником, и т.д.

Дискретная с.в. Х имеет распределение Пуассона, если она принимает значения 0, 1, 2, ..., m,... (счётное множество значений), а соответствующие вероятности выражаются формулой Пуассона:

λk_e−λ

p_k = P X(      = k) = ,                                                      (3) k!

Случайная величина Х, распределённая по закону Пуассона, имеет следующий ряд распределения:

xk	0	1	2	⋅ ⋅ ⋅	k	⋅ ⋅ ⋅
pk	e−λ			⋅ ⋅ ⋅	λke−λ  k!	⋅ ⋅ ⋅

где λ> ⁰ – параметр распределения. Распределение Пуассона является предельным для биномиального, когда n → ∞ и p → ⁰так, что произведение np =λ постоянно.

Можно доказать, что 

MX = DX =λ,                                                                          (4)

т.е. параметр распределения Пуассона равен одновременно математическому ожиданию и дисперсии случайной величины, имеющей это распределение. Это отличительная особенность изучаемого распределения, используемая на практике. На основании опыта находят оценки для MX и DX; если они близки между собой, то есть основание считать, что с.в. имеет распределение Пуассона.

• Равномерное распределение непрерывной случайной величины.

К случайным величинам, имеющим равномерное распределение, относятся такие, для которых все значения лежат внутри промежутка [a,b] и одинаково возможны, например,  время ожидания транспорта, курсирующего с определённым интервалом, равномерно распределено на этом интервале; ошибка округления результата измерения до ближайшего целого числа равномерно распределена на отрезке [−^{05 05}_{. , .} ].

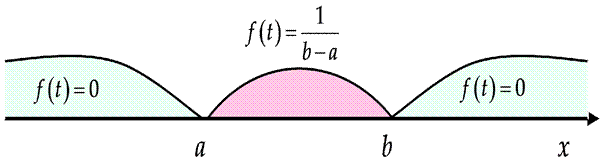
Непрерывная случайная величина Х равномерно распределена на отрезке [a,b], если её  плотность распределения вероятностей постоянна на данном отрезке, а вне его равна нулю:

c, a ≤ x ≤ b,                        1

f x( ) =                      , где с =                          .                                                     (5)

0, x < a, x > b                 b − a

График f x( ) имеет вид:

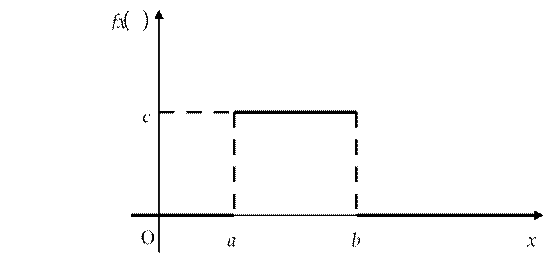
Вычислим математическое ожидание и дисперсию:

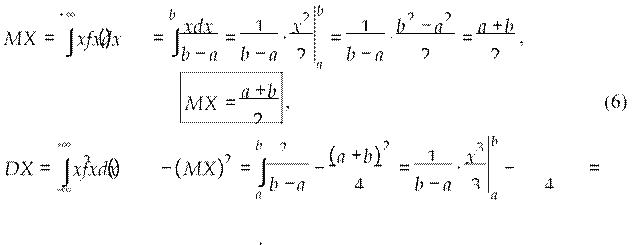
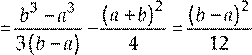              −∞                               a

x dx                                           (a + b)²

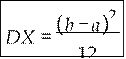 .                                                             (7)

x

Найдём функцию распределения F x( ) ⁼ ∫ f t dt( )           . Функция F x( )примет различные зна-

−∞

чения в зависимости от того, где на числовой оси расположена (⋅)x :

 

x                       x

1.  x < a, F x( ) ⁼ ∫ f t dt( )     ⁼ ∫ 0⋅dt = 0;

−∞                   −∞

x                       a                x                               x         − a

1              t           x

2.  a ≤ x ≤ b, F x( ) = ∫ f t dt( )         = ∫ 0⋅dt + ∫a              − adt = b − a a = b − a ;

b

−∞           −14243∞

=0

x                       a                 b                                 xb

₁                           t

3.  x > b, F x( ) ⁼ ∫ f t dt( )     ⁼ ∫ 0⋅dt ⁺ ∫ dt ⁺ ∫0⋅dt == 1.

−∞           −14243∞ a b − a 123b    b − a a

=⁰                                   =0

Получили:

0; x < a,

^x − a

F x( ) =  ; a ≤ x ≤ b .                                                             (8)  

b − a

1; x > b.

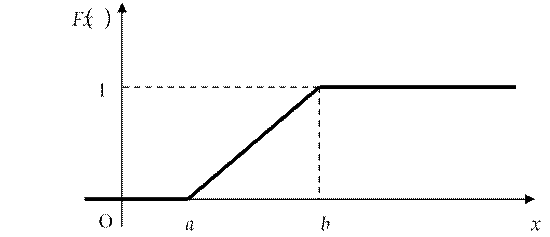
График F x( ) имеет вид:

Пример 2. Функция распределения непрерывной случайной величины изображена на рисунке:

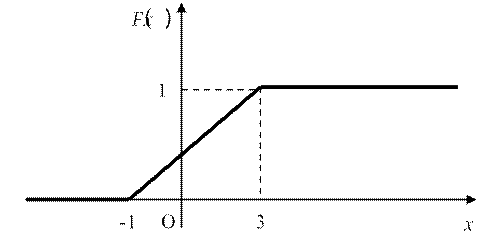
Найти: f x , MX, DX,( ) ^σ_X .

Решение. Это равномерное распределение  на отрезке