4. Лабораторная работа № 4
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКИХ
ЦЕПЕЙ
Для описания свойств электрических цепей при гармоническом воздействии используют частотные характеристики, понимая под ними отношение отклика V2 к входному воздействию V1 при различных частотах. Комплексная частотная характеристика (КЧХ) ЭЦ – это частотная зависимость отношения комплексной амплитуды отклика к комплексной амплитуде воздействия:
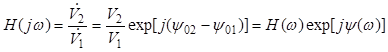 , (4.1)
, (4.1)
где H(ω) = V2/V1 – модуль КЧХ, который называется амплитудно-частотной характеристикой (АЧХ), а ψ(ω) = (ψ02 – ψ01) – аргумент КЧХ или фазочастотная характеристика (ФЧХ) электрической цепи.
Таким образом, частотные характеристики (АЧХ и ФЧХ) электрической цепи характеризуют ее способность к передаче от входа к выходу амплитуды и фазы гармонических воздействий различной частоты.
Для двухполюсников отношение отклика к
воздействию рассматривается на одной паре полюсов (выводов). Поэтому для них
вводятся входные КЧХ Z(jω) или Y(jω) с размерностью
сопротивления или проводимости. Подобные характеристики рассматривались выше
применительно к пассивным RLC двухполюсникам. То есть, если в качестве входного
воздействия, приложенного к пассивному двухполюснику, используется
синусоидальный ток (![]() ), а в качестве отклика –
напряжение на входных зажимах двухполюсника (
), а в качестве отклика –
напряжение на входных зажимах двухполюсника (![]() ), то в
соответствие с (4.1) входной КЧХ является входное сопротивление ЭЦ:
), то в
соответствие с (4.1) входной КЧХ является входное сопротивление ЭЦ: ![]() . Аналогично входную КЧХ пассивного
двухполюсника Y(jω) можно
определить как
. Аналогично входную КЧХ пассивного
двухполюсника Y(jω) можно
определить как ![]() .
.
Для описания свойств четырехполюсников используются
входные, выходные и передаточные КЧХ. В данной
лабораторной работе рассматриваются передаточные комплексные частотные
характеристики K(jω) пассивных четырехполюсников, определенных как
отношение комплексных амплитуд выходного и входного напряжений ![]() .
.
3.1.1. КЧХ электрических цепей первого порядка
Электрическими цепями первого порядка называются ЭЦ, содержащие только один реактивный элемент. Передаточная КЧХ таких цепей в общем случае может быть представлено выражением в виде отношения двух линейных полиномов с аргументом ω:
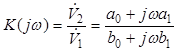 .
(4.2)
.
(4.2)
Тогда амплитудно-частотная характеристика (модуль КЧХ) и фазочастотная характеристика (аргумент КЧХ) электрической цепи можно вычислить по формулам:
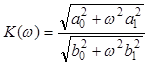 ;
(4.3)
;
(4.3)
![]() .
(4.4)
.
(4.4)
Рассмотрим два частных случая.
1. Пусть а1 = 0. Тогда из (4.2)-(4.4) следует:
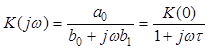 , (4.5)
, (4.5)
где K(0) = a0/b0 – коэффициент передачи ЭЦ по постоянному току (ω=0),
τ = b1/b0 – постоянная времени цепи;
АЧХ: 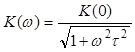 ; ФЧХ
; ФЧХ ![]() . (4.6)
. (4.6)
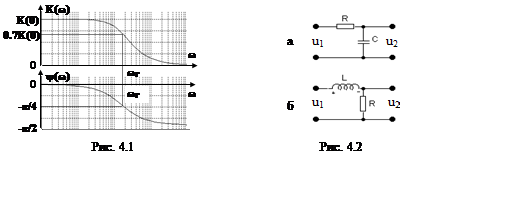
Графики АЧХ и ФЧХ (4.6) приведены на рис. 4.1. Частоту
ωг = 1/τ, на которой передаточная функция ЭЦ ![]() , называется граничной частотой полосы
пропускания цепи, а такую цепь называют низкочастотным звеном. Примером
пассивных низкочастотных звеньев служат ЭЦ, приведенные на рис. 4.2.
, называется граничной частотой полосы
пропускания цепи, а такую цепь называют низкочастотным звеном. Примером
пассивных низкочастотных звеньев служат ЭЦ, приведенные на рис. 4.2.
Для схемы рис. 4.2, а передаточная функция имеет вид:
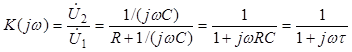 , (4.7)
, (4.7)
где τ= RC – постоянная времени RC-цепи, а коэффициент передачи ЭЦ по постоянному току K(0) = 1.
Для LR-цепи (рис. 4.2, б) КЧХ имеет вид:
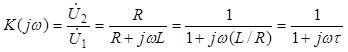 , (4.8)
, (4.8)
где постоянная времени LR цепи τ = L/R, а K(0) = 1.
 |
2. Пусть а0 = 0. Тогда из (4.2)-(4.4) получим:
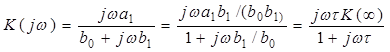 , (4.9)
, (4.9)
где K(∞) = K(ω = ∞) = a1/b1, τ = b1/b0 – постоянное время цепи.
АЧХ: 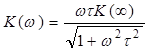 ; ФЧХ:
; ФЧХ: ![]() . (4.10)
. (4.10)
Графики АЧХ и ФЧХ (4.10) показаны на рис. 4.3. Частоту
ωг = 1/τ, на которой АЧХ ![]() ,
называется граничной частотой полосы пропускания цепи, а такую цепь
называют высокочастотным звеном. Примером пассивных высокочастотных
звеньев служат ЭЦ, приведенные на рис. 4.4.
,
называется граничной частотой полосы пропускания цепи, а такую цепь
называют высокочастотным звеном. Примером пассивных высокочастотных
звеньев служат ЭЦ, приведенные на рис. 4.4.
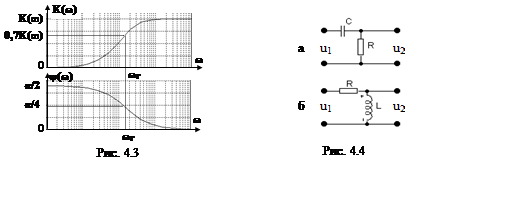
Комплексные частотные характеристики RC- и LR-цепи (рис. 4.4) соответственно определяются
выражениями:
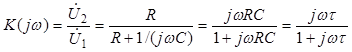 , (4.11)
, (4.11)
где τ= RC – постоянная времени RC-цепи, а K(∞) = 1.
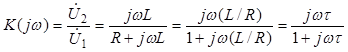 , (4.12)
, (4.12)
где постоянная времени LR-цепи τ = L/R, а K(∞) = 1.
Рассмотренные схемы являются простейшими фильтрами высокой частоты (ФВЧ) с нижней граничной частотой ωН = ωГ = .1/τ. Звено типа RC (рис. 3.4,а) при определенных условиях часто используется в качестве переходной цепи между каскадами усилителей или в качестве дифференцирующей RC-цепи.
3.1.2. КЧХ электрических цепей второго порядка
Электрическими цепями второго порядка называются ЭЦ, содержащие два реактивных элемента (однотипных или разнотипных). Передаточная КЧХ таких цепей в общем случае может быть представлена выражением в виде отношения двух квадратных полиномов с аргументом ω:
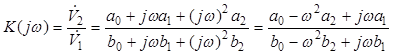 . (4.13)
. (4.13)
Тогда АЧХ и ФЧХ электрической цепи вычисляется по формулам:
АЧХ:
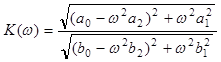 ;
(4.14)
;
(4.14)
ФЧХ:
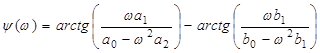 .
(4.15)
.
(4.15)
Для удобства анализа КЧХ числитель и знаменатель выражения (4.13) следует поделить на число, равное b2, оставив те же обозначения коэффициентов. Введя обозначения b2 = 1; b1 = 2σ; b0 = ω02, получаем:
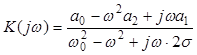 .
(4.13, а)
.
(4.13, а)
Тогда характеристическое уравнение имеет вид (p = jω):
![]() , (4.16)
, (4.16)
а корни характеристического уравнения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.