Частотные характеристики электрических цепей. Основные сведения. КЧХ электрических цепей первого порядка, страница 2

                                                                        (4.17)

определяют свойства цепи. При σ ≥ ω₀ корни p_1,2 являются действительными числами и ЭЦ является апериодической, т.е электрические процессы в цепи носит апериодический (монотонный) характер. Очевидно, что добротность цепи Q = ω₀/(2σ) ≤ 1/2. При σ ≥ ω₀ корни p_1,2  являются комплексными числами и электрические процессы в цепи приобретают колебательный характер с собственной частотой .

Примером ЭЦ второго порядка могут служить схемы, приведенные в разделе 2 (табл. 2.1). Расчет КЧХ (4.13) можно осуществить с помощью известных аналитических методов расчета (например, метод узловых потенциалов). При этом расчет КЧХ в общем случае может быть достаточно громоздким. Поэтому ограничимся рассмотрением частных случаев выражения (4.13).

1.  При a₂ = a₁ = 0 ЭЦ второго порядка приобретает свойства фильтра нижних частот и называется низкочастотным звеном второго порядка (НЧ-2). Комплексная частотная характеристика описывается выражением

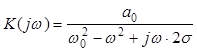,                                                                          (4.18)

а граничная частота определяется из условия K(ω_Г) = 0,707∙K(0), где K(0) = a₀/(ω₀²).

2.  При a₂ = a₀ = 0  КЧХ имеет вид:

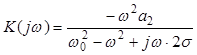,                                                                          (4.17)

а амплитудно-частотная характеристика такой ЭЦ соответствует АЧХ фильтра высоких частот. Поэтому такая электрическая цепь называется высокочастотным звеном второго порядка (ВЧ-2). Граничная частота определяется из условия K(ω_Г) = 0,707∙K(∞), где K(∞) = a₂.

3.  При a₂ = a₀ = 0 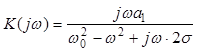  .                        (4.18)

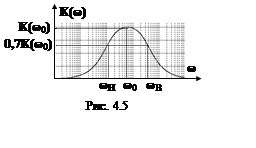
На рис. 4.5 приведен график АЧХ электрической цепи, называемой полосовым звеном , на котором показаны максимальное значение K(ω₀) = a₁/(2σ) и граничные частоты полосы пропускания ω_Г1 (ω_Н) и ω_Г2 (ω_В), определяемые из условия K(ω_Г) = 0,707∙ K(ω₀).

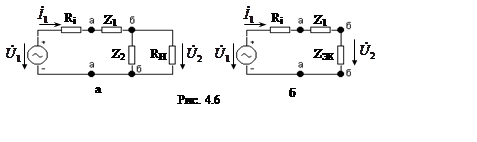
4.1.3. Влияние внутреннего сопротивления источника сигнала и сопротивления нагрузки на частотные характеристики ЭЦ

Рассмотренные выше частотные характеристики ЭЦ получены в режиме холостого хода на выходных зажимах цепи и без учета внутреннего сопротивления источника входного воздействия. Электрическая схема, показанная на рис. 4.6, а, содержит помимо самой электрической цепи второго порядка (элементы Z₁ и Z₂) источник синусоидального напряжения u₁ с внутренним сопротивлением R_i и нагрузку R_Н. Преобразуем электрическую схему к виду рис. 4.6, б, заменив параллельно соединенные элементы цепи Z₂ и R_Н эквивалентным сопротивлением Z_ЭК. Протекающий в цепи ток  равен: , а . Тогда КЧХ определяется как:

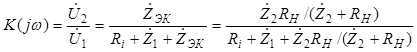.    (4.19)

Для ЭЦ первого порядка (рис. 4.2,  4.4) выражение (4.19) можно упростить, преобразовав его к виду (4.5) или (4.9), и найти соответствующие АЧХ и ФЧХ, а также параметры τ и ω_Г.

3.2. Подготовка к работе

Изучить материал рассматриваемой темы, используя конспект лекций, методические указания и соответствующие разделы учебников [1, 2]. Проверить степень усвоения материала, ответив на контрольные вопросы.

1. Рассчитать постоянную времени τ и граничную частоту ω_Г ЭЦ (рис. 4.6, а) без учета сопротивления нагрузки R_Н и внутреннего сопротивления источника напряжения R_i, выбрав вариант задания в соответствии с порядковым номером  студента в учебном журнале.

2.  Рассчитать указанные параметры с учетом  сопротивления нагрузки R_Н и внутреннего сопротивления источника напряжения R_i.

Таблица 4.1