Устойчивость фильтров. Рекурсивный фильтр. Кодирование чисел в ЦФ

Устойчивость фильтров

Фильтр называется устойчивым, если при любом ограниченном входном сигнале и любых начальных условиях выходной сигнал  тоже остается ограниченным при .

Т.е если , то  - ограничен.

Не рекурсивный фильтр всегда устойчив – это следует из разностного уравнения:

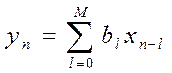 , то  получим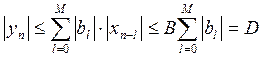

Рекурсивный фильтр устойчив тогда, когда устойчивым является решение соответствующего однородного линейного разностного уравнения:

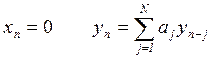
Решение 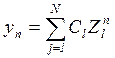 - это решение установившееся

 - характеристическое уравнение, если сумма конечная то фильтр устойчив, а это возможно когда . Основное свойство этих корней

РИСУНОК Z ПЛОСКОСТИ

Корни характеристического уравнения являются полюсами передаточной функции и для устойчивости фильтра они должны лежать внутри единичной окружности.

Устойчивость фильтра может обеспечиваться и если корни лежат на единичной окружности и даже вне ее при условии что здесь же расположены нули передаточной функции. Есть другое условие устойчивости:

Из интеграла Дюамеля 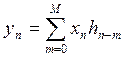, тогда для устойчивости надо чтобы  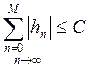- должна быть конечной.

Это все справедливо для линейного фильтра, т.е. где нет квантования и все операции точно. Реальный ЦФ является нелинейным, поэтому для него критерии устойчивости иные. Это важно, когда для представления сигнала используется малое число разрядов.

Кодирование чисел в ЦФ

Это актуально когда выполняется аппаратная реализация фильтра (без микропроцессора). Известно, что в цифровых устройствах для представления чисел прямой обратный и дополнительный коды. Операции сложения в ЦФ должны выполняться со знаком если использовать прямой код, то для реализации нужен отдельно сумматор и отдельно вычитающее устройство, поэтому и введен ДК. При выборе между ними надо учитывать, что переход в из ПК в ОК или ДК и обратно выполняется одинаково просто, но у ОК есть недостаток, заключающийся в том, что у него есть два нуля. В ЦФ этот недостаток не очень  существенный т.к. при этих вычислениях не нужно фиксировать факт равенства нулю какого-либо кода. Другой недостаток ОК - ему нужен циклический перенос при сложении кодов, поэтому если операция суммирования организуется последовательно (разряд за разрядом), то из-за циклического переноса длительность операции «+» оказывается в два раза дольше, чем в ДК. Поэтому операции сложения реализуются в ДК, а операции умножения проще реализуется в ПК, для этого и нужно преобразование кодов.

Важным для реализации является вопрос масштабирования, т.к. в цифровых устройствах распространенным способом записи чисел является формат с фиксированной запятой, в этом случае во всех регистрах используются одинаковые масштабы чисел, но это может привести к потере точности вычислений. Другой формат с плавающей запятой, здесь масштабы чисел в различных регистрах отличаются. Это увеличивает точность вычислений, но удлиняет процедуру, поэтому лучшим является промежуточный способ.

В этом случае масштабы чисел в регистрах одного звена одинаковы, это упрощает операции суммирования и умножения, а между звеньями есть масштабирование (масштабные множители), при этом обеспечивается наилучшая точность.

Особенности проектирования фильтров.

Проектирование фильтра заключается в организации требований к ИХ или ЧХ фильтра и нахождению условий обеспечивающих эти требования.

Но указанные требования не определяют однозначного требования к параметрам фильтра, поэтому задаются допустимые условия, позволяющие оптимизировать параметры фильтра в соответствии с заданным критерием. Чаще всего для оптимизации используют критерий минимума нужного количества ячеек памяти или критерий минимума количества алгебраических операций. При обеспечении заданных требований и характеристик фильтра, т.к. все свойства и характеристики ЦФ определяются значениями коэффициентов, входящих в разностное уравнение, их определяют по заданной ЧХ, а затем рассматривается возможность реализации этих коэффициентов с заданной точностью. Важно отметить, что нельзя получить ЦФ, ЧХ которого точно совпадает с заданной. Поэтому надо так его реализовывать, чтобы их расхождение было меньше некоторой величины, заданную ЧХ аппроксимируют с помощью некоторого выражения, позволяющего перейти к коэффициентам фильтра

Вся задача проектирования представляется тремя основными этапами: