Цель работы: изучение интерференции света, определение радиуса кривизны линзы и длины световой волны.
Приборы и принадлежности: микроскоп, плосковыпуклая линза и стеклянная пластина в специальной оправе, источник света, блок питания, фильтры.
Элементы теории и метод эксперимента:
При наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн.
Наблюдение интерференции возможно лишь в том случае, если интерферирующие световые волны когерентны, т.е. имеют одинаковые направления колебаний, частоту и постоянную во времени разность фаз.
Во всех интерференционных схемах получение когерентных световых волн достигается путём искусственного разделения световых волн, исходящих из источника, на две части. Последние в области перекрытия дают устойчивую интерференционную картину.
Пусть источники S1 и S2 посылают в точку О монохроматические волны:
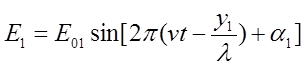
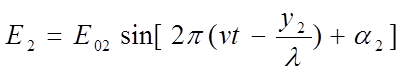
где ν – частота колебаний, λ – длина волны, излучаемая источниками, у1 и у2 – расстояния от источников до точки О, Е01 и Е02 – модули амплитуд светового вектора, α1 и α2 – начальные фазы колебаний источников.
Амплитуда Е0 результирующего колебания в точке О при наложении волн определяется по формуле:
![]()
где
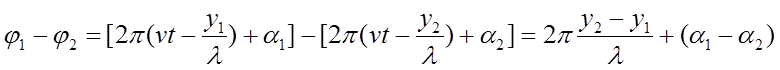 - разность фаз двух волн,
приходящих в точку С.
- разность фаз двух волн,
приходящих в точку С.
Учитывая, что интенсивность света в однородной среде пропорциональна квадрату амплитуды световой волны , получаем выражение для интенсивности:
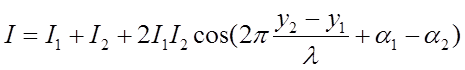
где I1 и I2 – интенсивности, создаваемые первой и второй волнами соответственно.
Если разность фаз возбуждаемых волнами колебаний непрерывно изменяется, принимая с равной вероятностью любые значения, то среднее значение cos(φ1-φ2) при этом обращается в нуль, интенсивности во всех точках складываются и интерференции не наблюдается.
Если разность фаз за время наблюдения остаётся постоянной, то волны ослабляют или усиливают друг друга. В точке С волны максимально усиливают друг друга, если разность фаз определяется как
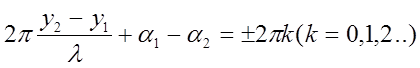
Тогда разность хода ![]() при
одинаковых начальных фазах определяет условие интерференционного максимума. В
этом случае
при
одинаковых начальных фазах определяет условие интерференционного максимума. В
этом случае ![]() .
.
Волны максимально ослабляют друг друга, если разность фаз
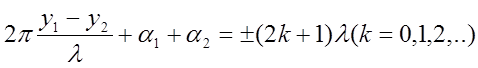
Тогда разность хода 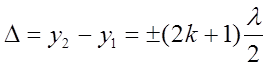 при α1=α2
определяет условие интерференционного минимума. В этом случае
при α1=α2
определяет условие интерференционного минимума. В этом случае![]() .
.
Интерференционная картина от клина переменной толщины впервые была изучена Ньютоном. Плосковыпуклая линза большого радиуса кривизны прижимается выпуклой стороной к плоской пластинке. Толщина воздушной прослойки h между пластиной и сферической поверхностью линзы увеличивается от точки соприкосновения к краям линзы. Места одинаковой толщины слоя воздуха расположены по концентрическим окружностям.
Пусть на линзу нормально падает пучок монохроматического света. Световые волны, отражённые от верхней и нижней границ воздушной прослойки, интерферируют между собой. В отражённом свете интерферирующие волны создают картину чередующихся концентрических светлых и тёмных колец с тёмным пятном в центре.
При нормальном падении света оптическая разность хода двух волн, одна из которых отражается от выпуклой поверхности линзы, другая – от верхней плоскости пластины, определяется по формуле:
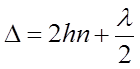
где h – толщина воздушного зазора; λ
– длина волны падающего света в вакууме; n – показатель
преломления прослойки; ![]() - дополнительная
разность хода, возникающая при отражении света от оптически более плотной
среды.
- дополнительная
разность хода, возникающая при отражении света от оптически более плотной
среды.
В зависимости от h оптическая разность хода Δ может содержать чётное или нечётное число полуволн. Это приводит к появлению в отражённом свете либо интерференционного максимума, либо минимума.
Учитывая, что в воздухе n=1, получаем:
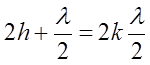
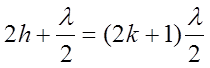
Толщина hk, соответствующая k-тому тёмному кольцу равна:
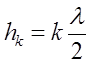
Получаем соотношение, связывающее толщину зазора, радиус кривизны и радиус
k-того кольца:
![]()
Принимая во внимание, что ![]() ,
получаем:
,
получаем:
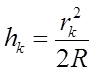
Из предыдущих соотношений следует:
![]()
Отсюда можно определить радиус кривизны линзы.
Однако практически трудно добиться идеального контакта
сферической поверхности линзы с плоской пластиной в одной точке вследствие
упругой деформации стекла и попадания в место их соприкосновения пылинок.
Поэтому непосредственно использовать формулу для вычисления R
нельзя. Действительно k-тому тёмному кольцу может
соответствовать не k-тый порядок интерференции, а (k+x), где x –
неизвестное целое число, одинаковое для всех колец. Для исключения возможной
ошибки радиус кривизны линзы R вычисляют по разности
квадратов радиусов колец ![]() и
и ![]() . В этом случае неизвестное x исключается. Пусть для колец с номерами k
и m имеем:
. В этом случае неизвестное x исключается. Пусть для колец с номерами k
и m имеем:
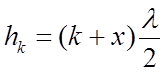
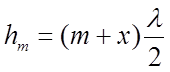
Тогда 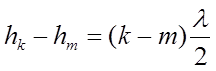
Ту же разность слоёв можно получить другим способом:
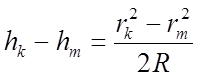
Из этого можно записать:
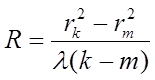
Переходя к диаметрам колец получаем:
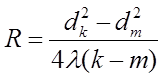
Анализ формулы показывает, что ![]() при
k-m=1, т.е. разность квадратов
диаметров двух любых соседних колец есть величина постоянная.
при
k-m=1, т.е. разность квадратов
диаметров двух любых соседних колец есть величина постоянная.
Следовательно, измерив диаметры нескольких тёмных колец и вычислив разность квадратов диаметров соседних колец, можно найти среднее значение для 4-5 пар колец.
Радиус кривизны вычисляем по формуле:
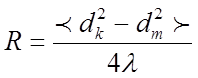
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.