1) Аппроксимация заданных характеристик фильтра, определение его алгоритма работы, определение ИХ и ЧХ фильтра.
2) Выбор разрядности при квантовании данных и коэффициентов фильтра
3) Определение нужной вычислительной производительности по заданным условиям и алгоритмам работы
Методы аппроксимации специализированы для рекурсивных и не рекурсивных фильтров. Поэтому различают задачу проектирования рекурсивных и не рекурсивных фильтров. В результате решения задачи аппроксимации становиться известными коэффициенты передаточной функции. Но свойства реального ЦФ на основе специального вычисления с ограниченной разрядностью могут существенно отличаться т.к. фильтр становиться нелинейным за счет усечения результатов вычисления и за счет переполнения регистров сумматора. Эти эффекты надо учитывать при проектировании фильтра.
В итоге выбранная разрядность кодов определяет погрешность реализации.
Элементы проектирования не рекурсивных фильтров
Разновидности не рекурсивных фильтров и требования к ним
РИСУНОК СХЕМКИ
1) N – четное, а коэффициенты симметричные ![]()
2) N – нечетное, а коэффициенты симметричные ![]()
3) N – четное, а коэффициенты антисимметричные ![]()
4) N – нечетное, а коэффициенты антисимметричные ![]()
Минимально фазовые – нули внутри и на единичной окружности, они используются в качестве изрп фильтров тогда когда групповое время замедления должно быть малым.
Основные этапы проектирования не рекурсивных фильтров
Этапы:
1) Формулировка задачи аппроксимации, надо выполнить:
а. Выбор
типа фильтра б. Выбор
аппроксимирующей функции ![]() , которая задает
требования к ЧХ
, которая задает
требования к ЧХ
в. Выбор
аппроксимирующей функции ![]() , она зависит от вектора
параметров с – это вектор коэффициентов фильтра или как-то с ним вязан г. Выбор
критерия аппроксимации, т.е.
, она зависит от вектора
параметров с – это вектор коэффициентов фильтра или как-то с ним вязан г. Выбор
критерия аппроксимации, т.е. ![]()
д. Определение
весовой функции аппроксимации ![]() , которая задает требования
к точности аппроксимации
, которая задает требования
к точности аппроксимации
Цель первого этапа – математическая формулировка задачи, вычисление вектора с по заданным требованиям к характеристикам фильтра.
2) Решение задачи аппроксимации:
а. Оценка нужного прядка фильтра N
б. Расчет вектора коэффициентов с в. Проверка критерия по отношению к полученному решению, т.е. заданных требований к характеристикам фильтра, если выясняется, что требования к характеристикам выполнено, то по вектору с определяются характеристики фильтра, если выясняется что требования к характеристикам не выполнено, то надо увеличивать порядок фильтра и повторять вычисления.
Цель второго этапа определение коэффициентов фильтра
3) Расчет разрядности коэффициентов (определение разрядности регистров ПЗУ). Этот этап зависит от выбранной элементной базы. Если реализуем фильтр на МП, то здесь определяется соответствует ли разрядность выбранного процессора требуемой, если не соответствует, то лучше процессор большей разрядности или повторить синтез при большем порядке фильтра, если фильтр реализуется аппаратно, то min разрядность уменьшать до тех пор пока выполняются требования к характеристикам фильтра.
4) Расчет разрядности регистров ОЗУ. Выполняется так, чтобы мощность собственных шумов фильтра была меньше , чем мощность входных шумов.
5) Схемная реализация фильтра на выбранной базе
Формулировка задачи аппроксимации. Критерии аппроксимации
Целью решения задачи
аппроксимации является определение коэффициентов ![]() передаточной
функции фильтра. Для решения этой задачи аппроксимируемая функция
передаточной
функции фильтра. Для решения этой задачи аппроксимируемая функция ![]() должна удовлетворять требованиям:
должна удовлетворять требованиям:
1) ![]() простая зависимость от вектора с
простая зависимость от вектора с
2) ![]() при заданных
при заданных ![]() .
.
Исходя из этих требований наиболее простой аппроксимацией является линейная зависимость.
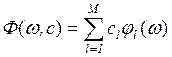 , где
, где ![]() - набор базисных функций. Существует два
основных критерия аппроксимации:
- набор базисных функций. Существует два
основных критерия аппроксимации:
1) Среднеквадратический критерий
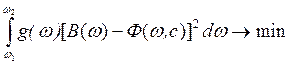 ,
подбирая коэффициенты с
,
подбирая коэффициенты с
2) Наилучший равномерный или Чебышевский критерий
![]()
Эти критерии применяются либо по
отдельности, либо вместе. Общий критерий определяется весовой функцией ![]() , чем точнее выполняется равенство
, чем точнее выполняется равенство ![]() , тем выше
, тем выше ![]() (т.е.
даем больший вес нужной частоте).
(т.е.
даем больший вес нужной частоте).
При использовании Чебышевского критерия --------- отдельных подынтервалов частот:
![]()
![]() , где R –
произвольная постоянная, она постоянна для всех подынтервалов частот.
, где R –
произвольная постоянная, она постоянна для всех подынтервалов частот.
![]()
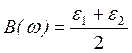
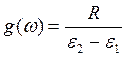
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.