Пусть в схеме, приведенной на рис. 1.10,: R1= 0,1 кОм; R2 =10 кОм; R3 = 3 кОм; R4= 0,2 кОм; R5= 2 кОм; R6= 5,6 кОм; R7= 4 кОм; R8= 6 кОм; E1 = 12 В; E2 = 2 В; I = 0,1 А.
 Найдем параметры эквивалентного
генератора, заменяющего активный двухполюсник. Для расчета внутреннего
сопротивления преобразуем схему активного двухполюсника (заменив идеальные
источники энергии их внутренними сопротивлениями) к виду пассивного
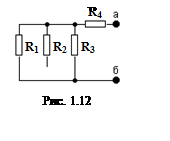
двухполюсника (рис. 1.12).
Найдем параметры эквивалентного
генератора, заменяющего активный двухполюсник. Для расчета внутреннего
сопротивления преобразуем схему активного двухполюсника (заменив идеальные
источники энергии их внутренними сопротивлениями) к виду пассивного
двухполюсника (рис. 1.12).
Очевидно, что Ri = R4 + R1R3/(R1 + R3)= = 0,2 + 0,1*3/(0,1 + 3) = 0,297 (кОм).
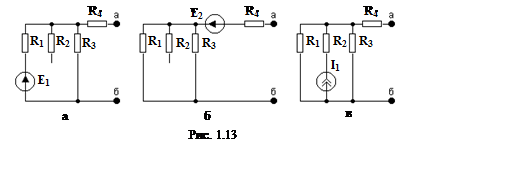
Схемы для расчета эквивалентной ЭДС методом наложения для каждого из источников
электрической энергии приведены на рис. 1.13. Для схемы (рис. 1.13, а) Eэкв1 = Uаб = UR4 + UR3.
Поскольку в режиме холостого хода ток через сопротивление R4
равен нулю, то UR4 = 0, а
напряжение на сопротивлении R3 определяется по правилу
делителя напряжения: UR3 = E1*R3/(R1 +R3).
Поэтому, с учетом направления тока IR3
получаем Eэкв1 =UR3
= 12*3/(0,1+3) = 11,613 (В).
В схеме (рис. 1.13, б) ток не протекает, т.к. нет замкнутого контура, содержащего источник ЭДС E2. Поэтому Eэкв2 = -E2 = -2 (В).
В схеме с идеальным источником тока (рис. 1.13, в) ток, вырабатываемый источником, протекает через параллельно соединенные сопротивления R1 и R3. Согласно правилу деления тока ток в резисторе R1 равен IR1 = I*R3/(R1 +R3). Тогда падение напряжения на R1: UR1 = IR1*R1 = I*R1R3/(R1 +R3) = 0,1*100*3000/(100+3000) = = 9,667 (В). С учетом направления тока, протекающего через R1 получаем Eэкв3 = Uаб = UR1 = 9,667 (В). ЭДС эквивалентного генератора Eэкв = Eэкв1 + Eэкв2 + Eэкв3 = 11,613 – 2 + 9,667 = 19,28 (В).
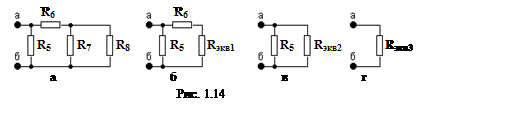 |
Используя правила замены последовательно и параллельно соединенных элементов цепи, находим:
Rэкв1 = R7*R8/(R7 + R8) = 4∙103*6∙103/(4∙103 + 6∙103) = 2,4 кОм;
Rэкв2 = R6 + Rэкв1 = 5,6∙103 + 2,4∙103 = 8∙103 = 8 кОм;
Rэкв3 = R5*Rэкв2/(R5 + Rэкв2) = 2∙103*8∙103/(2∙103 + 8∙103) = 1,6 кОм.
Таким образом, входное сопротивление пассивного двухполюсника Rвх = Rэкв3 = 1,6 кОм.
Напряжение на входе пассивного двухполюсника Uаб (рис. 1.11) находим по правилу делителя напряжения (1.4):
![]()
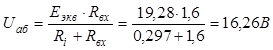 .
.
Поскольку ко входу пассивного двухполюсника (рис. 1.10) и его эквивалентным схемам (рис. 1.14) приложено напряжение Uаб = 1б,26 В, то теперь мы можем найти токи и напряжения на элементах пассивного двухполюсника.
Ток Iп, потребляемый двухполюсником, определим по закону Ома:
Iп = IRвх = Uаб/Rвх = 16,26/(1,6∙103) = 10∙10-3 =10,16 мА.
Учитывая, что Ri и Rвх соединены последовательно(рис.1.11), то IRi = IRвх = I = 10,16 мА, а URi = IRi∙Ri = 3,02 В.
Аналогично находим токи, протекающие через резистор R5 и эквивалентное сопротивление Rэкв2 (рис. 1.14, в):
IR5 = Uаб/R5 = 16,26/(2∙103) = 8∙10-3 = 8,13 мА;
Iэкв2 = Uаб/Rэкв2 = 16,26/(8∙103) = 2∙10-3 = 2,03 мА.
Падение напряжение на R5 равно UR5 = Uаб = 16,26 В.
Так как Rэкв2 – это эквивалентное сопротивление последовательно соединенных R6 и Rэкв1 (рис. 1.14, б), то IR6 = Iэкв1 = Iэкв2 = 2,03 мА.
Падение напряжения на R6 и Rэкв1 находим по закону Ома:
UR6 = IR6∙R6 = 2,03∙10-3*5,6∙103 = 11,37 В;
Uэкв 1= Iэкв1*Rэкв1 = 2,03∙10-3*2,4∙103 = 4,87 В.
Так как UR7 = UR8 = Uэкв1 = 4,87 В, то токи, протекающие через резисторы R7 и R8, равны:
IR7 = UR7/R7 = 4,87/(4∙103) = 1,22∙10-3 = 1,22 мА;
IR8 = UR8/R8 = 4,87/(6∙103) = 0,81∙10-3 = 0,81 мА.
Полученные результаты расчета сведем в таблицу, предварительно вычислив мощности, потребляемые каждым резистором.
Таблица 1.3
|
Ri |
Rвх |
R5 |
R6 |
R7 |
R8 |
|
|
I, мА |
10,16 |
10,16 |
8,13 |
2,03 |
1,22 |
0,81 |
|
U, В |
3,02 |
16,26 |
16,26 |
11,37 |
4,87 |
4,87 |
|
P, мВт |
30,68 |
165,20 |
132,19 |
23,08 |
5,94 |
3,94 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.