Электрические цепи постоянного тока. Электрическое сопротивление и емкость. Идеальный источник напряжения, страница 4

Всякий пассивный двухполюсник является потребителем электрической энергии и характеризуется одной величиной – входным сопротивлением R_вх, поэтому на эквивалентной схеме его можно заменить одним резистивным элементом с сопротивлением R = R_вх. Если известна схема пассивного двухполюсника, то для определения входного сопротивления R_вх нужно тем или иным способом ее «свернуть» относительно двух заданных выводов, например, поочередно используя рассмотренные выше правила замены последовательно или параллельно соединенных элементов одним эквивалентным.

Активный двухполюсник можно «свернуть» до так называемого эквивалентного генератора – эквивалентного источника напряжения (ЭИН) с параметрами E_экв = U_хх и  R_i = R_аб или эквивалентного источника тока (ЭИТ) с параметрами I_экв = I_кз и R_i = R_аб. Сопротивление  R_аб есть входное сопротивление рассматриваемого двухполюсника при условии замены всех идеальных источников активного двухполюсника их внутренними сопротивлениями (т.е. ИИН заменяют идеальным проводником, а ИИТ – разрывом цепи). Напряжение холостого хода U_хх определяется как напряжение в точках эквивалентного преобразования а и б при отключении нагрузки в этих точках (режим холостого хода). Если в выделенной цепи имеется нескольких источников, то для нахождения U_хх обычно применяют метод наложения. Ток короткого замыкания I_кз равен току в точках преобразования а и б при их коротком замыкании и определяется также по методу наложения.

Метод наложения базируется на справедливом только в линейных ЭЦ принципе суперпозиции: в линейной ЭЦ отклик (реакция) на сумму воздействий равен сумме откликов (реакций) на каждое их воздействие.

Метод наложения может быть сформулирован следующим  образом [1]: ток (напряжение) в i-ой ветви активной линейной ЭЦ равен алгебраической сумме токов (напряжений) в этой ветви, создаваемых каждым источником в отдельности, при условии, что все остальные источники заменены своими внутренними сопротивлениями.

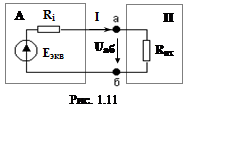
С учетом вышесказанного электрическую схему, приведенную на рис. 1.10, можно заменить эквивалентной схемой, состоящей из эквивалентного генератора  и резистивной нагрузки ( рис. 1.11).

Мощность, отдаваемая эквивалентным активным двухполюсником (рис. 1.11), равна             P_A = E_экв∙I, а мощность, потребляемая пассивным двухполюсником  –  P_П = R_вх∙I². При R_i ≠ 0 всегда P_А > P_П, т.е. часть энергии теряется в активном двухполюснике (мощность потерь P_i = R_i∙I). Очевидно, что P_А = P_i + P_П, поэтому можно записать выражение [1]

                                         (1.8)

Для нахождения тока I, при котором мощность P_П максимальна, найдем производную функции (1.8) по I и приравняем ее нулю:

откуда искомый ток I = E_экв/2R_i. С другой стороны ток, протекающий в ЭЦ (рис. 1.11),  I = E_экв/(R_i+R_вх). Приравняв правые части последних выражений получаем : 2R_i = R_i + R_вх или R_вх = R_i. 

Таким образом, мощность, передаваемая от активного двухполюсника к пассивному, зависит от соотношения входных сопротивлений этих двухполюсников и достигает максимума при условии равенства этих сопротивлений. Т.е. приR_вх = R_i максимальная потребляемая мощность P_{П макс} = E²_экв/4R_вх.

КПД эквивалентного активного двухполюсника определяется как:

               (1.9)

Из (1.9) следует, что при максимальной потребляемой пассивным двухполюсником мощности КПД равен 0,5. Более высокое значение КПД может быть достигнуто при R_вх > R_i. Следует отметить, что КПД реального активного двухполюсника равен КПД эквивалентного только при выполнении определенного условия, а именно: если при отключении пассивного двухполюсника от реального активного в ветвях последнего не будет токов и потерь, так же как и в эквивалентной схеме на рис. 1.11. В противном случае КПД реального активного двухполюсника меньше КПД эквивалентного.

1.2. Подготовка к работе

Изучить материал рассматриваемой темы, используя конспект лекций, методические указания и разделы 1 и 2 учебника [1]. Проверить степень усвоения материала, ответив на контрольные вопросы.