Электрические цепи постоянного тока. Электрическое сопротивление и емкость. Идеальный источник напряжения, страница 3

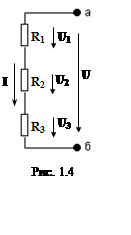
Последовательно соединенные элементы цепи образуют делитель напряжения (рис. 1.4). Можно сформулировать следующее правило делителя напряжения: отношение напряжений на последовательных элементах цепи равно отношению сопротивлений этих элементов. Например, для последовательного участка цепи, показанной на рис. 1.4, имеем: I= U₁/R₁ = U₂/R₂ = U₃/R₃; т.е. U₁/U₂ =  R₁/R₂; U₂/U₃ = R₂/R₃; U₁/U₃ = R₁/R₃.

Учитывая (1.1), можно записать:

I = U/R_Э = U/(R₁ + R₂ + R₃).

Тогда, по правилу делителя напряжения можно получить выражения для напряжений на каждом из ее последовательно соединенных элементов:

       (1.2)

2) 

Замена нескольких параллельно соединенных сопротивлений одним эквивалентным. Элементы электрической цепи соединены параллельно, если к ним приложено одно и то же электрическое напряжение (рис. 1.5). При параллельном соединении элементов электрической цепи их проводимости складываются:

.                          (1.3)

Параллельно соединенные элементы цепи образуют делитель тока.Можно сформулировать следующее правило делителя тока: отношение токов в параллельных ветвях цепи равно отношению проводимостей этих элементов. Например, для трех параллельно соединенных резисторов (рис. 1.6), к каждому из них приложено одно и тоже напряжение U, следовательно, U = I₁/G₁ = I₂/G₂ = I₃/G₃. Отсюда следует, что I₁/I₂ = G₁/G₂; I₂/I₃ = G₂/G₃; I₁/I₃ = G₁/G₃.

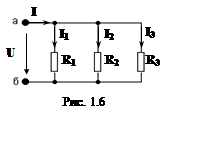Учитывая (1.3), можно записать: U = I/G_Э = I/(G₁ + G₂ + G₃). Тогда, по правилу делителя тока получим выражения для токов в каждом из  последовательно соединенных элементов:

               (1.4)

3) Преобразование РИН в РИТ и наоборот (рис. 1.7).

Из условия эквивалентности преобразования, т.е. равенства токов и напряжений в резистивной нагрузке R реальных источников напряжения и тока (рис. 1.7, а и б), и с учетом (1.2) и (1.4) получяем 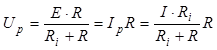, откуда    (1.5)

Используя соотношения (1.5) и зная параметры РИН (E и R_i) можно при необходимости заменить его эквивалентной схемой РИТ и наоборот, зная параметры РИТ можно заменить его схемой РИН. Идеальные источники тока и напряжения не взаимозаменяемы.

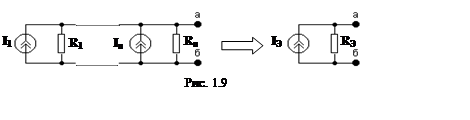
4) Замена нескольких последовательно соединенных РИН одним эквивалентным (рис. 1.8). При последовательном соединении РИН эквивалентная ЭДС схемы замещения равна алгебраической сумме  ЭДС источников (с учетом направлений), а внутреннее сопротивление эквивалентного РИН равна сумме внутренних сопротивлений этих источников:

                           (1.6)

5) Замена нескольких параллельно соединенных РИТ одним эквивалентным (рис. 1.9). При пораллельном соединении РИТ величина тока эквивалентного источника тока равна алгебраической сумме  токов источников (с учетом направлений), а внутренняя проводимость эквивалентного РИТ равна сумме внутренних проводимостей этих источников:

               (1.7)

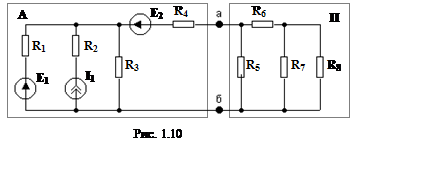
При исследовании процессов в сложной электрической цепи (например, для установления связи между одной частью электрической цепи, содержащей источники электрической энергии, и другой частью с приемниками энергии) иногда возникает необходимость выделить из ЭЦ отдельные ветви. Часть электрической цепи произвольной конфигурации с двумя выделенными выводами или полюсами называют двухполюсниками. Например, в схеме на рис. 1.10 относительно выводов а и б выделены два двухполюсника.

Двухполюсники, содержащие источники электрической энергии, называются активными, а двухполюсники, не содержащие источников электрической энергии, - пассивными [2]. На рис. 1.10 активный и пассивный двухполюсники обозначены соответственно буквами А и П.