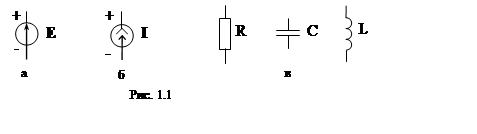Электрические цепи постоянного тока. Электрическое сопротивление и емкость. Идеальный источник напряжения, страница 2

Идеальный источник тока (рис. 1.1, б) создает ток I (A), величина которого не зависит от подключенной к нему нагрузки (величины напряжения на нем). И так как в режиме холостого хода ИИТ допускает бесконечно большое напряжение U, то ИИТ обладает бесконечно большой мгновенной мощностью. Внутренняя проводимость идеального источника тока G_i = 0 (R_i = 1/G_i = ∞).

Резистивный элемент (рис. 1,1,в) обладает способностью только поглощать электрическую энергию, преобразуя ее в другие виды энергии (тепловую, световую, механическую и др.) при потребляемой мощности P = U_R∙I_R, где  U_R – падение напряжения на сопротивлении R резистивного элемента при протекании через него тока I_R. Учитывая, что по закону Ома  U_R = R∙I_R, то потребляемую  мощность можно  представить  в  виде  P = R∙I_R² = U_R²/R.

Реальные источники напряжения (РИН) и тока (РИТ) отличаются от идеальных (ИИН и ИИТ) наличием внутреннего сопротивления        R_i ≠ 0, которое подключено последовательно к ИИН (рис. 1.2, а) и параллельно к ИИТ (рис. 1.2, б). На этом же рисунке показаны подключенные к выводам (а-б)источников нагрузочные резисторы R.

К основным законам теории электрических цепей, на базе которых построены все методы анализа и синтеза ЭЦ, относятся первый и второй законы Кирхгофа и закон Ома. Известный из школьного курса физики закон Ома для участка цепи получен опытным путем и устанавливает взаимосвязь тока, напряжения и сопротивления (проводимости) для любого элемента электрической цепи:                       I = U/R = U∙G.

Для расчета сложной ЭЦ вводятся понятия узла, ветви и замкнутого контура. Ветвью электрической цепи называется участок схемы, состоящий только из последовательно включенных источников ЭДС и приемников с одним и тем  же протекающим через них током. Узлом цепи называется место или точка соединения трех и более ветвей (иногда узлом называют и точку соединения двух ветвей). Замкнутый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза.

Первый закон Кирхгофа: Алгебраическая (с учетом знака) сумма токов для любого узла схемы равна нулю, т.е. сколько тока «втекает» в узел по одним ветвям (эти токи берутся со знаком «+»), столько из него и «вытекает» по другим ветвям (эти токи берутся со знаком «-»).

Второй закон Кирхгофа: Алгебраическая сумма падений напряжений на элементах в любом контуре равна нулю, т.е. алгебраическая сумма ЭДС в контуре равна алгебраической сумме падений напряжений на пассивных элементах этого контура.

Эквивалентные преобразования электрических цепей

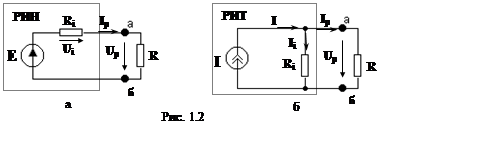
Для удобства анализа линейной электрической цепи часто используют эквивалентные преобразования ее топологии. Для пассивных ЭЦ условием эквивалентности является неизменность сопротивлений и проводимостей в точках преобразования, т.е. новая (преобразованная) схема должна обладать тем же сопротивлением (проводимостью), что и исходная электрическая цепь. Условием эквивалентности преобразования одной активной электрической цепи (РИН или РИТ) в другую является неизменность токов и напряжений в точках преобразования.

Ниже приводятся правила основных преобразований участков электрической цепи, в основе которых лежат законы Кирхгофа и Ома.

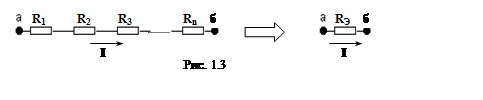
1)  Замена нескольких последовательно соединенных сопротивлений одним эквивалентным. Элементы электрической цепи соединены последовательно, если через них протекает один и тот же электрический ток (рис. 1.3). При последовательном соединении элементов их сопротивления складываются и при необходимости их можно заменить в электрической цепи эквивалентным сопротивлением:

R_Э = R₁ + R₂ + R₃ +…+Rn                                                                     (1.1)