Основные характеристики речевого сигнала и требования к телефонному тракту. Принцип действия угольного микрофона, страница 12

Число точек коммутации при двухзвенной схеме T=TА+TВ=64+64=128, таким образом, двухзвенная схема решает ту же коммутационную задачу, что и однозвенная схема, но содержит в два раза меньше точек коммутации. В других звеньевых включениях может оказаться еще больше сокращение числа точек коммутации. Сокращение числа точек коммутации в звеньевых включениях объясняется более высоким использованием каждой точки коммутации. Если в однозвенных включениях каждая точка обеспечивает соединение одного входа с одним выходом, то в звеньевых включениях одна точка звена А коммутации позволяет соединить вход с различными выходами.

При этом в звеньевых включениях увеличиваются потери сообщения из-за внутренних блокировок, когда некоторые свободные выходы не могут быть подключены ко входам определенного коммутатора звена А из-за занятости промежуточных линий, необходимых для данного соединения.

Коммутационная схема, в которой могут быть внутренние блокировки, называется блокирующей коммутационной схемой.

Внутренние блокировки увеличивают число отказов в соединении и снижают пропускную способность коммутационной системы. При рациональном построении звеньевой схемы это снижение будет в пределах нормы.

Звеньевые включения характеризуются следующими структурными параметрами:

-  число коммутаторов звена А  (К_А);

-  число входов в один коммутатор звена А  (n_A);

-  число выходов из одного коммутатора звена А (m_A);

-  число коммутаторов звена В  (K_B);

-  число входов в один коммутатор звена В  (n_B);

-  число выходов из одного коммутатора звена В (m_B);

-  коэффициент связности (f_AB);

-  коэффициент расширения (сжатия) (σ).

С помощью этих параметров можно получить следующие простые соотношения:

-  число входов коммутационной системы :

-  число выходов коммутационной системы ;

-  общее число промежуточных линий .

Коэффициент связности или просто связность представляет собой количество промежуточных линий, связывающих каждый коммутатор звена А с каждым из коммутаторов звена В. При связности  справедливы соотношения , . Покажем двухзвенную схему со связностью(рис. 9.16) 

Рис. 9.16. Двухзвенная схема со связностью коммутационной системы

Связность равна

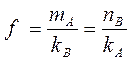                                                     .                                                   (9.1)

Общее число точек коммутации в двухзвенной схеме определяется из выражения

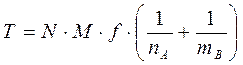.                                      (9.2)

Например, при связности  и в двухзвенной схеме получаем число точек , а в однозвенной схеме , т. е. в 5 раз больше.

Под коэффициентом расширения (сжатия) понимают

, где  – число промежуточных линий, N – число входов коммутационной системы. Если  , то имеет место расширение на звене А, т. е. переход от меньшего числа линий к большему и наоборот при имеет место сжатие. Коэффициент определяет пропускную способность блока.

Построение коммутационных систем в значительной степени определяется режимом искания (свободное, групповое, линейное). Чаще всего используются двухзвенные блоки.

16. Объясните преимущества неблокирующих полнодоступных многозвенных схем по сравнению с однозвенными.  Приведите соотношение, связывающее число входов и выходов в отдельном коммутаторе неблокирующего коммутационного блока.

В рассмотренных ранее звеньевых включениях имели место внутренние блокировки.

Покажем возможность построения неблокирующих коммутационных блоков, т. е. блоков, в которых отсутствуют внутренние блокировки. Оказывается, как доказал Клоз, при условии симметричная, трехзвенная, односвязная схема будет полнодоступной и неблокирующей (рис. 9.19).

Рис. 9.19. Неблокирующий коммутационный блок

Проанализируем количество точек коммутации для однозвенной и трехзвенной полнодоступной схемы без блокировок при разном количестве входов N (табл. 9.1)

Таблица 9.1