Множества. Элементы множества. Отношения между множествами. Операции над множествами, страница 4

Следствие (теоремы о СНДФ). Любую функцию алгебры логики можно представить контактной схемой.

СЛОЖНОСТЬ ФОРМУЛ И СХЕМ

Поскольку существуют различные  формулы, представляющие одну и ту же функцию, различные схемы, представляющие одну и ту же формулу, то естественно возникает вопрос о сложности формул и схем.

Под сложностью формулы можно понимать:

а) число вхождений переменных в формулу, б) число операндов &, Ú,   в формуле.

Под сложностью схемы из функциональных элементов будем понимать число функциональных элементов в схеме.

Под сложностью контактной схемы будем понимать число контактов в схеме.

Пример. Упростить систему (уменьшить число уравнений или неравенств):

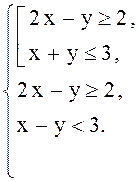
Сопоставим выражению  логическую переменную А , а выражению   – переменную В. Тогда наша система примет вид  . Упрощая, получаем:

.

Следовательно, исходная система эквивалентна системе

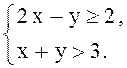
Пусть задана схема из функциональных элементов &, Ú, . Требуется ее упростить, т.е. создать другую схему с меньшей сложностью, реализующей ту же функцию алгебры логики. Для этого надо записать формулу, соответствующую схеме, и упростить ее (минимизировать количество операндов в базисе &, Ú, ). После этого строится схема для упрощенной формулы.

Пример. Упростить формулу.   

1. 2. 3. 4. 5.

Сложность схемы равна пяти. Упрощаем формулу:

.

Сложность последней формулы и соответствующей ей схемы равна 2. Кроме закона поглощения, при упрощении схем из функциональных элементов используются законы де Моргана, т.к. замена  на , а также  на  уменьшает сложность формулы на одну единицу.

Пример. Пусть дана контактная схема

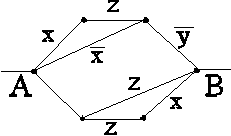
и требуется ее упростить, т.е. создать другую контактную схему с меньшей сложностью,  но реализующую ту же функцию алгебры логики. Функция проводимости схемы:

.

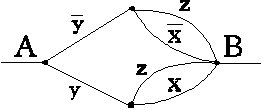
Исходная схема имела сложность 8. Эквивалентная ей схема имеет сложность 6:

Задание 1. а) А, В, С – множества, х – элемент множества.  Доказать или опровергнуть.

1.	а) Если   и , то .	б) .
2.	а) Если , то .	б) .
3.	а) Если  , то .	б) .
4.	а) Если  , то  и .	б) .
5.	а) Если   и  А    В , то .	б) Если , то .
6.	а) Если  или , то .	б) .
7.	а) Если , то .	б) .
8.	а) Если , то  и .	б) .
9.	а) Если , , то .	б) .
10.	а) Если  или , то .	б) Если , то .
11.	а) Если  и , то .	б) .
12.	а) Если  и , то .	б) .
13.	а) Если , то .	б) Если , то .
14.	а) Если , то  и .	б) .
15.	а) Если , то .	б) .
16.	а) Если  или , то .	б) .
17.	а) Если  и , то .	б) .
18.	а) Если , то .	б) Если , , то .
19.	а) Если , то .	б) Если , то .
20.	а) Если , то .	б) Если , то .
21.	а) Если , то .	б) .
22.	а) Если  и , то .	б) .
23.	а) Если , то .	б) .
24.	а) Если , то .	б) .
25.	а) Если , то .	б) .
26.	а) Если  и , то .	б) .
27.	а) Если , то .	б) .
28.	а) Если , то .	б) .
29.	а) Если , то .	б) Если , то .
30.	а) Если  или , то .	б) .