![]()
(совершенная дизъюнктивная нормальная форма) .
Имеет место также двойственное к СДНФ представление логических функций как произведение дизъюнкций:
Теорема.
Если ![]() , то
, то
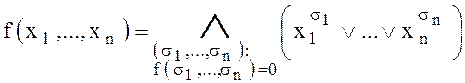
– совершенная конъюнктивная нормальная форма (СКНФ).
Пример. Написать совершенную конъюнктивную нормальную форму для функции:
|
x, y, z |
F (x, y, z) |
x, y, z |
F (x, y, z) |
|
0 0 0 0 0 1 0 1 0 0 1 1 |
1 0 1 0 |
1 0 0 1 0 1 1 1 0 1 1 1 |
0 1 1 1 |
Функция имеет три нуля и поэтому
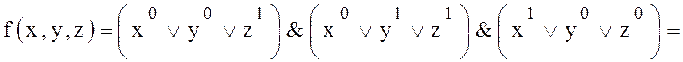
![]()
– совершенная конъюнктивная нормальная форма.
Из формулы (2) видно, что в СДНФ при фиксированных значениях переменных может быть отлично от нуля не более одного слагаемого. Поэтому в этой формуле знак дизъюнктивной суммы можно заменить на знак суммы пo mod 2:
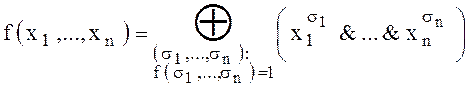 .
.
Но ![]() .
Отсюда получаем
.
Отсюда получаем
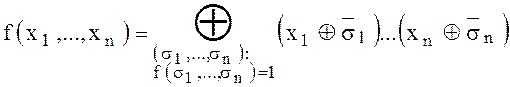 , что после раскрытия скобок и
приведения подобных слагаемых и даст полином Жегалкина.
, что после раскрытия скобок и
приведения подобных слагаемых и даст полином Жегалкина.
Следствие (теоремы о СНДФ). Любая функция алгебры логики представима полиномом Жегалкина.
Пример. Функцию
|
x, y, z |
F (x, y, z) |
x, y, z |
F (x, y, z) |
|
0 0 0 0 0 1 0 1 0 0 1 1 |
0 1 0 1 |
1 0 0 1 0 1 1 1 0 1 1 1 |
0 0 1 0 |
записать полиномом Жегалкина.
СНДФ данной функции
![]() .
.
Следовательно,
![]() .
.
Раскрывая
скобки и используя свойства коммутативности, ассоциативности и дистрибутивности
операции ![]() , а также учитывая, что
, а также учитывая, что ![]() для любой функции g ,
выводим:
для любой функции g ,
выводим:
![]() .
.
Пример.
Преобразовать формулу ![]() в полином Жегалкина. Выразим
встречающиеся операции через логическое умножение, сложение по mod 2
и логическую константу 1:
в полином Жегалкина. Выразим
встречающиеся операции через логическое умножение, сложение по mod 2
и логическую константу 1: ![]()
![]()
![]() . Подставляя в формулу и
упрощая, получаем:
. Подставляя в формулу и
упрощая, получаем:
![]()
![]() .
.
Определим схему из функциональных элементов в базисе
&, Ú, ![]() .
.
1. Функциональный элемент является схемой, если его входам приписаны имена
переменных, выходу приписана одна из функций &, Ú, ![]() ,
которая выполняется этим элементом:
,
которая выполняется этим элементом:
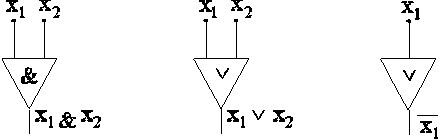
2. Пусть имеется две схемы
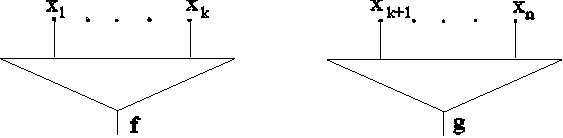
реализующие
функции ![]() ,
, ![]() . Тогда
схемы
. Тогда
схемы
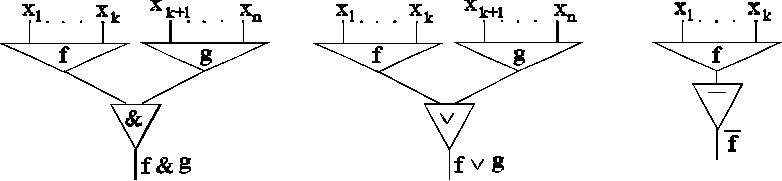
реализуют
функции ![]() ,
, ![]() ,
, ![]() соответственно.
соответственно.
3.
Схемой из функциональных элементов в базисе &, Ú, ![]() является
также схема
является
также схема
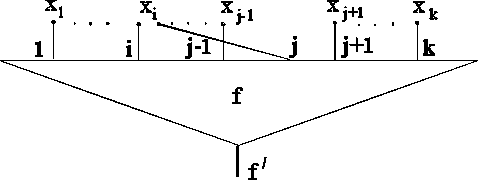
реализующая
функцию ![]() , у которой i-й и j-й
входы соответствуют одной переменной
, у которой i-й и j-й
входы соответствуют одной переменной ![]() .
.
Пример.
Рассмотрим формулу ![]() . Она может быть представлена
схемой из функциональных элементов:
. Она может быть представлена
схемой из функциональных элементов:
|
|
1.
2.
3.
4.
5.
|
Схема содержит пять операндов, как и формула . Однако на выходах 1 и 2 реализуются одинаковые функции. Если в схеме «склеить» два конъюнктора в один, то получится более простая схема, использующая только четыре операнда:
|
|
1.
2.
3.
4.
|
Этот простой пример показывает, что одинаковые формулы могут изображаться различными схемами.
И наоборот, если дана схема из функциональных элементов, то по ней можно написать формулу.
Пример. Следующей схеме
|
|
1.
2.
3.
4.
5.
6.
7.
|
соответствует
функция ![]() .
.
Будем рассматривать формулы в базисе &, Ú, ![]() , у
которых отрицание стоит только над простыми переменными.
, у
которых отрицание стоит только над простыми переменными.
Параллельно-последовательные контактные схемы (p-схемы) можно определить по
формулам в базисе &, Ú, ![]() индуктивно:
индуктивно:
а) переменным х, ![]() ставим
в соответствие схемы:
ставим
в соответствие схемы:

–
граф с одним ребром (с приписанным символом х или ![]() )
и двумя вершинами, называемыми полюсами контактной схемы; б) если
)
и двумя вершинами, называемыми полюсами контактной схемы; б) если
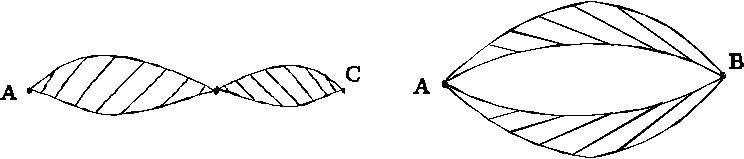
–
контактные схемы с полюсами А, B и D, C для формул А, B
соответственно, то формулам ![]() ,
, ![]() будут отвечать схемы с полюсами A, C и A, B.
будут отвечать схемы с полюсами A, C и A, B.
Под функцией алгебры логики, соответствующей схеме, понимается дизъюнкция всех путей (конъюнкций элементов пути), соединяющих полюсы. Такая функция называется функцией проводимости схемы.
Кроме параллельно-последовательных, существуют контактные схемы более общего вида.
Пример.Рассмотрим контактную схему
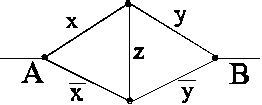
По этой схеме можно выписать соответствующую формулу:
![]() .
.
Эту формулу можно реализовать в виде p-схемы:
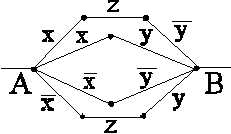
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.