Множества. Элементы множества. Отношения между множествами. Операции над множествами, страница 2

Функция & называется конъюнкцией двух переменных  х,  y  или логической операцией «и».

Функция Ú называется дизъюнкцией двух переменных  х,  y  или логической операцией «или».

Функция Å называется суммой по модулю 2 от двух переменных  х,  y  или логической операцией «исключенное или».

Функция  х Þ у  называется  импликацией  и  читается «из х следует y», «х влечет y», «если х, то y».

Функция  х ½ у  называется функцией Шеффера или штрихом Шеффера.

Функция  х у  называется стрелкой Пирса.

Функция  х º у  называется эквивалентностью или равносильностью, иногда обозначается,  как  Û  и читается  «х эквивалентно y», «х тогда и только тогда  y», «для х  необходимо и достаточно  y».

Функция  называется инверсией или отрицанием  х  и читается «не х».

Функция  х, у  являются простыми переменными.

Константы 0, 1 могут рассматриваться как постоянные функции от переменных х, у.

Справедливы следующие тождества:

1) ,

(x & y) =  (y & x),

  –  коммутативность;

2) , 

(x & y) & z = x & (y & z),

  –  ассоциативность;

3)  & z = (x & z) Ú (y & z),

(x & y)  &,

 & z = (x & z) Å (y & z)  –  дистрибутивность; 

4) (x & х) = х ,

 –  идемпотентность;

5) ,

  – законы де Моргана;

6)  , , ;

7) , ;

8)   ;

9)   ;

10) , , ;

11)  .

Все соотношения проверяются непосредственно с помощью таблицы 1.

В дальнейшем мы будем иногда опускать знак логического умножения: .

Некоторый набор функций алгебры логики  называется полной системой или базисом, если любую другую функцию можно выразить через функции этого набора. Чтобы записать некоторую формулу в заданном базисе, надо выразить все функции, входящие в формулу, через функции базиса, а затем подставить.

Пример. Выразить функцию  в базисе  – штрих Шеффера.

В силу 6, 7  и 10, см. выше, имеем:

, , откуда

.

ЗАКОН ДВОЙСТВЕННОСТИ

Функция   называется двойственной к функции . Из определения следует, что если в таблице истинности для  нули заменить единицами, а единицы – нулями (включая аргументы), то мы получим таблицу для двойственной функции  . Таким образом, можно убедиться в двойственности функции      и  т.п.

В силу закона двойного отрицания  получаем , т.е. отношение двойственности взаимно и симметрично.

Функция f  называется самодвойственной, если .

Верна теорема двойственности:

Теорема. Пусть

.

Тогда

.

Теорема показывает, что если функция задана формулой в каком-то базисе, то двойственная функция задается в базисе из двойственных функций формулой, имеющей ту же структуру.

Так из первого закона де Моргана   и теоремы двойственности следует второй закон де Моргана .

Пример. Используя теорему двойственности, перейдем к двойственной формуле для функции

.

Так как     то     и

.

СДНФ  и  СКНФ

Введем обозначение 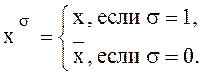 Легко проверить, что  при   и    при .

Элементарной конъюнкцией называется форма 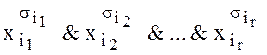, где –  константы, равные 0 или 1. Уравнение

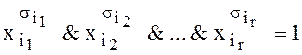
равносильно системе 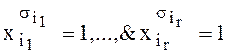 и, следовательно, системе ,.

Элементарная конъюнкция  называется совершенной относительно переменных .

Теорема. Если , то

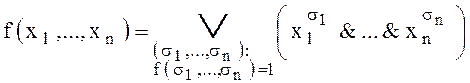                     (2)

(суммирование производится по всем наборам , на которых функция принимает значение 1) – совершенная дизъюнктивная нормальная форма (СНДФ).

Пример. Написать совершенную дизъюнктивную нормальную форму для функции:

x, y, z	F (x, y, z)	x, y, z	F (x, y, z)
0 0 0 0 0 1 0 1 0 0 1 1	0 1 0 1	1 0 0 1 0 1 1 1 0 1 1 1	1 0 0 0

Функция имеет три единицы. Им отвечают совершенные элементарные конъюнкции   . По теореме получаем: