Допустим, что он двигался в течение времени t/2 от Земли со скоростью V, а затем возвращался на Землю то же время со скоростью -V. Время t измерено по земным часам. Не подлежит сомнению, что возвращался именно космонавт, потому что в момент поворота он, а не земной наблюдатель, испытывал силы инерции. Поэтому время космонавта t равно
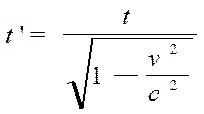
Если когда-нибудь удастся достичь скорости, равной 0.99 скорости света, то t’ = 1/7 t, и за семь земных лет космонавт проживет один год.
Не следует думать, что выигрыш во времени достигается космонавтом во время ускорения: можно повернуть назад, путешествуя и год, и десять лет с одной и той же скоростью. Но во втором случае выигрыш будет в 10 раз больше, а ускорение при повороте — одно и то же. Следовательно, разница времен только реализуется благодаря ускорению, а набирается во время полета.
Конечно, чтобы выигрыш был сколько-нибудь осязаемым, скорость космонавта должна быть очень близкой к скорости света, что пока очень далеко от возможностей техники. Но известны опытные факты, относящиеся к удлинению времени жизни — только не людей, а элементарных частиц.
В космических лучах присутствуют быстрые частицы, пи-мезоны, которые самопроизвольно распадаются на более легкие мю-мезоны и нейтральные частицы. Медленные пи-мезоны живут до распада в среднем две стомиллионные доли секунды: таково среднее время жизни пи-мезона в связанной с ним системе отсчета; Если бы это время было одинаковым относительно любой системы отсчета, то самые быстрые пи-мезоны, летящие почти со скоростью света, могли бы в среднем пролетать в воздухе расстояние около 6 м до своего распада. Фактически быстрые пи-мезоны пролетают в воздухе в среднем гораздо большие расстояния, так что относительно системы отсчета, связанной с Землей, время существенно удлиняется.
Рассмотрим теперь, что делается с твердым масштабом при движении. Для этого снова обратимся к рис. 25. Совместим левый конец стержня с началом координат O, а правый конец поместим в точку В1 лежащую на оси абсцисс. Иначе говоря, мы приняли, что в системе отсчета, относительно которой стержень покоится, моменты времени для обоих концов стержня одинаковы. Это вполне естественно, так как концы покоятся друг относительно друга. Что же будет происходить во всех других системах отсчета?
Будем по-прежнему считать, что левый конец в начальный момент времени находился в начале координат любой системы отсчета. В тот же момент времени в системе, где стержень покоится, сделаем засечку правого конца B1 на масштабе, который движется относительно данного. Все эти засечки будут лежать на кривой В\В2, имеющей асимптотами те же световые прямые 00', что и кривые А1А2. Засечки левого и правого концов стержня будут не одновременными относительно движущихся систем отсчета. Более того, существуют такие системы, где вторая засечка произошла раньше первой, и такие, где она произошла позже. Но нет ни одной системы, где бы обе засечки произошли в одной и той же точке пространства, т. е. где длина стержня равна нулю.
Пусть все стержни снабжены мерными делениями. Тогда, делая засечку, наблюдатель, неподвижный относительно стержня, заметит, что против его десятого деления находится, например, двадцатое или сотое деление движущегося стержня, смотря по положению точки В1,, иначе говоря, для него движущийся масштаб сократится. В одном его делении будут два, или десять, или сто движущихся. Не обязательно говорить о делениях, нанесенных человеком, это могут быть природные деления, например постоянные кристаллической решетки одного и того же вещества.
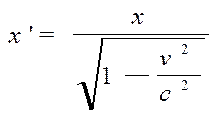
Если положить t = 0:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.