brows fields f2:28:h=, Раб. отметка в конце участка, , h:36:h=, Длина участка, следующего за отметкой, WINDOW wff all format COLOR SCHEME 10 set color to gr+/b, w+/r, b
do while. t.
n1=0
n2=0
n3=0
mm=1
@ 14,11 menu mv, 3,4 title , Выбор нужного режима работы,
read menu to save
do case
case mm=1
sele 3
go top
do while. not. eof( )
n3=n3+1
z5(n3)=f2
z6(n3)=h
q=(f1=f2)/2
if q<=0
c=(1,5*q**2-(4,4=b)*q+0,9)*h
y=y+c
n1=n1+1
z1(n1)=c
z2(n1)=y
f1=f2
else
if q-6<=0
a=(1,5*q**2+b*q+0,7)*h
x=x+a
n2=n2+1
z3(n2)=a
z4(n2)=x
f1=f2
else
if x-12<0
a=(1,75*q**2+(b-3)*q+9,7)*h
x=x+a
n2=n2+1
z3(n2)=a
z4(n2)=x
f1=f2
else
a=(2*q**2+(b-9)*q+45,7)*h
x=x+a
n2=n2+1
z3(n2)=a
z4(n2)=x
f1=f2
endif
endif
endif
skip
enddo
save screen to aaa
clear
wait , Установите бумагу. Нажмите кл. «ENTER»
clear
set device to print
set printer to a4. txt
clear
@ 0,0 to 24,80 double
@ 0,15 say, Объем земляных работ по средним рабочим отметкам ,
@ 2,12 say, Ширина основной площадки , +str(b. 7,2)
@ 3,12 say, Начальный объем насыпи , +str(xx. 7,2)
@ 4,12 say, Начальный объем выемки , +str(yy. 7,2)
@ 5,12 say, Рабочая отметка в начале участка , +str(ff1. 7,2)
@ 7,12 say, Рабочая отметка в конце участка ,
ns=8
do prt with z5, n3, 10, ns
@ ns, 12 say , Длины участков, следующие за этими отметками,
ns=ns+1
do prt with z6, n3, 10, ns
@ ns, 12 say , Объемы выемок на участках,
ns=ns+1
do prt with z1, n1, 10, ns
@ ns, 12 say , Объемы выемок с нарастающим итогом,
ns=ns+1
do prt with z2, n1, 10, ns
@ ns, 12 say , Объемы насыпи на участках,
ns=ns+1
do prt with z3, n2, 10, ns
@ ns, 12 say , Объемы насыпи с нарастающим итогом,
ns=ns+1
do prt with z4, n2, 10, ns
eject
set device to screen
restore screen from aaa
set color to gr+/b, w+/r,b
case mm=2
clear
exit
otherwise
clear
return
end case
end do
end do
set color to gr+/b, w+/r,b
return
proc pod
set color to W+/N
@ 18,20 say ,F1,
@ 18,20 say ,F2,
@ 18,30 say ,F3,
@ 18,40 say ,ESC,
set color to GR+/W
@ 18,22 say ,Добавить,
@ 18,32 say ,Удалить,
@ 18,42 say ,Восст.,
@ 18,52 say ,Выход,
set color to
return
PROC V1X
KEYBOARD CHR(23)
return
proc ppp
append blank
return
proc prt
para a, n, l, ns
dime a(n)
i=1
do while. t.
for j=4 to l*8-1 step 8
@ ns, j say str(a(i), 8,2)
i=i+1
if i>n
ns=ns+1
return
end if
end for
ns=ns+1
end do
Результаты расчетов
Объем земляных работ по средним рабочим отметкам
Ширина основной площадки 6,50
Начальный объем насыпи 0.
Начальный объем выемки 0.
Рабочая отметка в начале участка 2,48
Рабочие отметки в конце участка
3.25 3.25 10.00 0.00 -7.13 -5.34
Длины участков, следующих за этими отметками
0.90 1.55 1.00 0.75 0.80 0
Объемы выемок на участках
47.06 0
Объем выемок с нарастающим итогом
47.06 47.06
Объем насыпи на участках
28.47 58.39 116.92 53.03
Объем насыпи с нарастающим итогом
28.47 86.86 203.78 256.80
2 ТЯГОВЫЕ РАСЧЕТЫ
2.1 Общие положения
Тяговые расчеты проводятся с целью определения значений скорости, времени хода и механической работы локомотива. Они нужны для технико-экономической оценки проектных решений и расчета пропускной способности железных дорог. Ниже излагается методика тяговых расчетов.
С помощью вычислительной техники можно решать и такие частные задачи тяговых расчетов, как, например, определение основного сопротивления движению, подсчет удельных равнодействующих сил при различных режимах работы локомотива, определение массы состава из условия равномерного движения поезда на руководящем (расчетном) подъеме и с учетом кинетической энергии поезда, установление допускаемых скоростей по тормозам и др. Использование ПК (персональных компьютеров) особенно эффективно, когда расчеты носят исследовательский характер и выполняются при различных вариантах исходных данных.
Как известно, решение большинства задач тяговых расчетов основано на интегрировании уравнения движения поезда. Расчеты на ЭВМ в этом отношении не являются исключением. В основе численных методов лежит допущение постоянства удельных равнодействующих сил в пределах небольших интервалов пути, или скорости, или времени. Практика расчетов показала, что по методическим соображениям интегрирование по пути с постоянным шагом Δs наиболее целесообразно.
При составлении программы расчетов для численного решения дифференциального уравнения движения поезда принят известный в математике метод Эйлера. Рассмотрим его применительно к наиболее характерному случаю движения поезда под тягой, которому соответствует уравнение
|
dv/dt = 120(fк - w), |
(2.1) |
или (при небольших приращениях скорости и времени)
|
Δv/Δt = 120(fк - w). |
(2.2) |
Пусть известна функция – кривая v =f(t) (рисунок 2.1), проходящая через точку 1 с координатами vн и tн (начальное условие). Проведем к кривой
v =f(t) в точке 1 касательную и отметим на ней точку 2, соответствующую моменту времени tк. Угловой коэффициент tgα выражается формулой (2.2). Скорость в конце интервала времени Δt
|
vк = vн + Δv |
(2.3) |
Очевидно, чем меньше t, тем меньше полученное значение vк (точка 2) будет отличаться от истинного (точка 2').
Подставляя в выражение (2.3) значение Δv из формулы (2.2), получим
|
vк = vн +120(fк - w)н Δt. |
(2.4) |
Формула (2.4) непосредственно не может быть использована для расчетов, поскольку она включает в себя неизвестную величину приращения времени. Примем изменение скорости в пределах Δt по линейному закону.
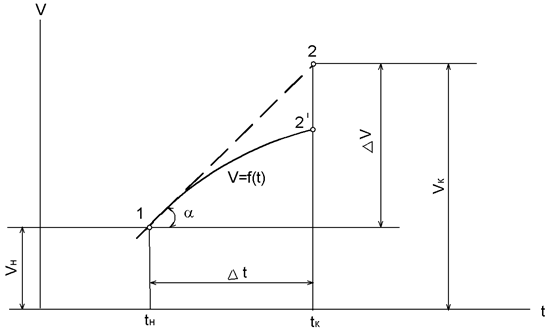
Рисунок 2.1 – Расчетная схема к численному интегрированию уравнения
движения поезда
Тогда отрезок пути, соответствующий Δt, будет
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.