Как логично и связно вписать математическую модель –
в текст курсовой или дипломной работы. Пример.
2.1. Анализ эффективности результатов деятельности
столовой «Ромашка»
<…..>
Поэтому возрастает роль другой причины, вызвавшей значительное изменение—увеличение—прибыли—снижения уровня издержек производства и обращения. Следовательно, анализ этого фактора имеет особое значение, так как именно его воздействие способствовало росту прибыли. Для определения степени влияния изменения уровня издержек на сумму прибыли составляется математическая модель зависимости данных показателей.
Математическая модель строится на основе данных результатов экономической деятельности столовой «Ромашка»: показателей прибыли и издержек—за 2003год (таблица 2.1.2.). Моделируется статистическое уравнение зависимости прибыли предприятия от издержек на основе данных за год.
Таблица 2.1.2.
Значения прибыли и издержек столовой «Ромашка» по месяцам за 2003 год.
|
Месяц |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
Июль |
Август |
Сентябрь |
Октябрь |
Ноябрь |
Декабрь |
|
Прибыль (У) |
185 |
190 |
200 |
220 |
235 |
89 |
35 |
28 |
235 |
237 |
278 |
265 |
|
Издержки (Х) |
6231 |
7955 |
8114 |
8151 |
8792 |
1606 |
370 |
275 |
8792 |
9150 |
9340 |
9292 |
Суть метода заключается в определении коэффициентов сравнения факторных (X) и результативных (Y) признаков путем отношения отдельных значений каждого из признаков к его минимальному или максимальному уровню.
В качестве факторного признака X – издержки, а в качестве результативного признака Y – прибыль.
Чтобы определить возможные форму и направление связи (прямую и обратную) между X и Y строится график (Рис.2.1.1), значения факторного признака предварительно ранжируются и им в соответствие записываются величины результативного признака (таблица 2.1.3.)
Таблица 2.1.3.
Значения прибыли и издержек столовой «Ромашка» за 2003 год,
ранжированные по прибыли
|
Прибыль (У) |
28 |
35 |
89 |
185 |
190 |
200 |
220 |
235 |
237 |
250 |
265 |
278 |
|
Издержки (Х) |
275 |
370 |
1606 |
6231 |
7955 |
8114 |
8151 |
8792 |
9150 |
9262 |
9292 |
9340 |
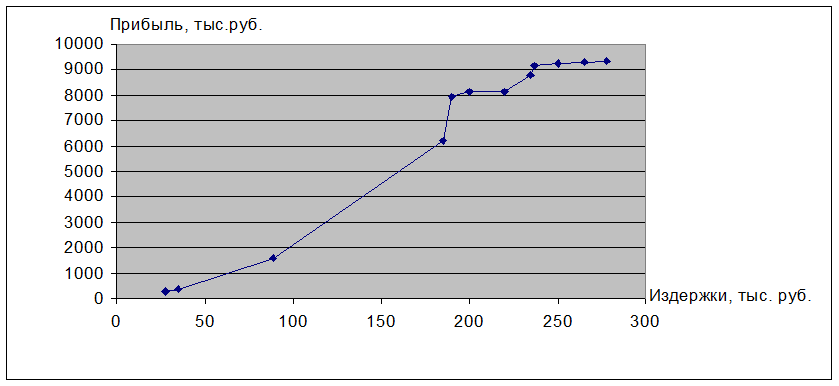
Рис.2.1.1. График зависимости прибыли столовой «Ромашка» от издержек за 2003 год.
Из графика видно, что зависимость можно описать линейным уравнением. Так как при увеличении факторного признака X увеличивается результативный признак Y, можно сказать, что связь между факторами – прямая. Следовательно, принимается за базу сравнения минимальные уровни факторов, Xmin = 275 и Ymin=28 (таблица 2.1.4.)
Прямая при увеличении факторного и результативного
признаков описывается уравнением: 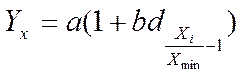 , где a = Ymin
, где a = Ymin
Вычисление значений осуществляется в форме таблицы 2.1.4.
Таблица 2.1.4.
Расчет уравнения прямой зависимости прибыли и издержек столовой «Ромашка» за 2003 год.
|
Y |
X |
Хi/Xmix-1=dx |
yi/ymin-1=dy |
b*dxi/xmin-1, bdx |
Теоретические значения, Yx |
|
275 |
28 |
0 |
0 |
0 |
28 |
|
370 |
35 |
0,25 |
0,3454545 |
1,0208684 |
56,584315 |
|
1606 |
89 |
2,1785714 |
4,84 |
8,8961388 |
277,09189 |
|
6231 |
185 |
5,6071429 |
21,658182 |
22,896619 |
669,10535 |
|
7955 |
190 |
5,7857143 |
27,927273 |
23,625811 |
689,52271 |
|
8114 |
200 |
6,1428571 |
28,505455 |
25,084195 |
730,35745 |
|
8151 |
220 |
6,8571429 |
28,64 |
28,000961 |
812,02692 |
|
8792 |
235 |
7,3928571 |
30,970909 |
30,188537 |
873,27902 |
|
9150 |
237 |
7,4642857 |
32,272727 |
30,480213 |
881,44597 |
|
9262 |
250 |
7,9285714 |
32,68 |
32,376112 |
934,53113 |
|
9292 |
265 |
8,4642857 |
32,789091 |
34,563687 |
995,78323 |
|
9340 |
278 |
8,9285714 |
32,963636 |
36,459585 |
1048,8684 |
|
67 |
273,59273 |
Определяются коэффициенты сравнения X и Y путем отношения их отдельных значений к минимальным
уровням: от dx1=X1\
Xmin до dх12=X1\ Xmin и от dy1=Y1\Ymin до dy12=Y1\ Ymin (таблица). Коэффициенты сравнения показывают, что,
например, прибыль в январе на 15% выше,
чем в базовом месяце—августе; а уровень издержек в этом месяце выше на 226% по
сравнению с базовым. Расчет коэффициентов сравнения результативного признака Y осуществляется с учетом изменения его значений: при
увеличении: 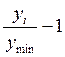 (таблица
2.1.4.)
(таблица
2.1.4.)
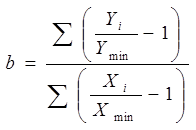 |
Свободный параметр a – это минимальное значение результативного признака (Ymin).
В результате получается следующее уравнение: YХ = 28(1+4,0834*Dxi/xmin-1)
Оценка устойчивой или неустойчивой связи между факторами и
результативным признаком проводится по шкале зависимости на основе расчета коэффициента
устойчивости связи. 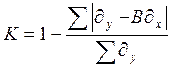
Вспомогательные расчеты коэффициента устойчивости приведены в таблице 2.1.5..
Таблица 2.1.5.
Расчет коэффициента устойчивости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.