Изменение приведённой скорости и коэффициент восстановления полного давления воздуха вдоль трубы

Министерство образования и науки Украины

Сумский государственный университет

Кафедра технической теплофизики

Обязательное домашнее задание

по дисциплине

 «Спецразделы теплофизики»

Студент                                                                                      Ховяков Е. Ю.

Группа                                                                                                        К-71

Вариант                                                                                                         29                                                                     

Проверил                                                                                     Ванеев С.М.                                                                     

Сумы 2011

Содержание

                                                                                                                          С.

1 Исходные данные………………………………………………………………..2

2 Расчет… ………………………………………………………………………….4

2.1 Определение режима течения в трубе…...………………..……………….4

2.2 Определение приведенной длины трубы………………………..…..…….4

2.3 Определение изменение приведенной скорости……………………….…5

2.4 Определение коэффициента восстановления полного                             давления воздуха вдоль трубы……………….…………………………..…….6

3 Исходные данные………………………………………………………………..8

4 Расчет… ………………………………………………………………………….9

4.1 Определение приведенной длины трубы…………………………….…..9

4.2 Критическая приведенная длина трубы………………………………....9

4.3 Определение  приведённой скорости  на входе из трубы…………….10

4.4 Определение местоположения скачка уплотнения…………………….11

4.5 Определение  изменения статического давления по длине трубы……12

1 Исходные данные

Воздух вытекает из бака в атмосферу через суживающееся сопло, соединённое с теплоизолированной трубой. Давление и температура в баке поддерживаются постоянными и равными , . Приведённая скорость на входе в трубу. Определить режим течения в трубе. Найти приведённую длину трубы, изменение приведённой скорости и коэффициент восстановления полного давления воздуха вдоль трубы. Потерями энергии в коническом сопле пренебречь (=).

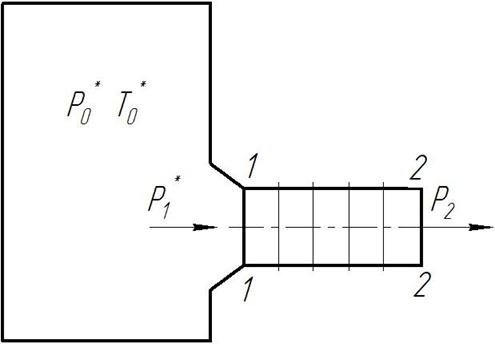
      Рисунок 1 – Расчетная схема истечения воздуха из бака

   2 Расчет     

       Система уравнений для адиабатического течения газа с трением в трубе постоянного сечения имеет следующий вид:

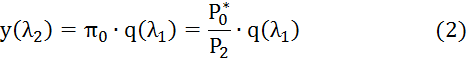
где  – приведённая скорость на выходе из трубы;

        – располагаемое отношение давлений;

        – газодинамическая функция;

       -вспомогательная функция.

2.1 Определяем режим течения в трубе:

При =0,8 по газодинамическим функциям

где ГДФ приведенного расхода;

Находим

Найдем располагаемое отношение давления:

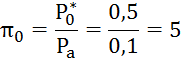
 где  - атмосферное давление.

По таблицам газодинамических функций для получения значения  находим - режим течения сверхзвуковой, что не может быть, тогда:

 и  – поток на выходе звуковой.

2.2 Находим приведенную длину трубы. Приведенная длина трубы равна критической длине.

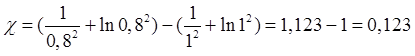
2.3 Определение изменения приведенной скорости.

Разбиваем участок от   до  на 6 сечений с шагом 0,04

Участок 1 при

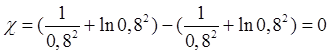
Участок 2 при

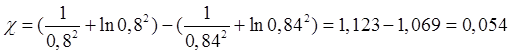
Участок 3 при

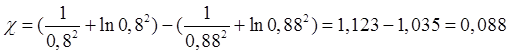
Участок 4 при

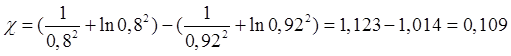
Участок 5 при

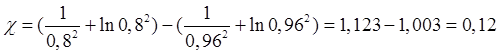
Участок 6 при

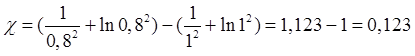
Результат расчета сведены в таблицу 1.

Таблица 1 – Изменение приведённой скорости от приведённой длины

	0,8	0,84	0,88	0,92	0,96	1
	0	0,054	0,088	0,109	0,12	0,123

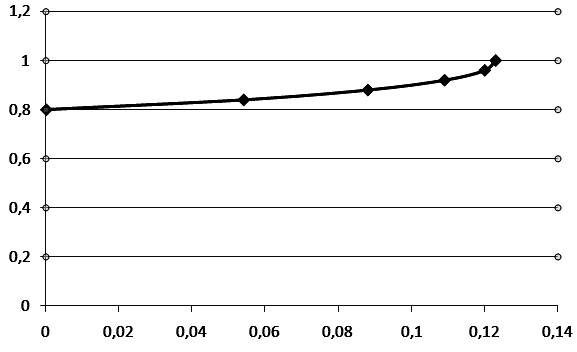
Рисунок 2 – Изменение приведенной скорости вдоль трубы

2.4 Определение коэффициента восстановления полного давления воздуха вдоль трубы:

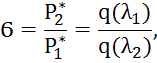
где - расходная характеристика

Определим   вдоль трубы при определенных  :

При  по газодинамическим функциям q(λ₂)=0,9518

                                   

 При   q(λ₂)=0,9691

                                     

При   q(λ₂)=0,9826

                                     

При   q(λ₂)=0,9923

                                     

При   q(λ₂)=0,9981

                                     

При  q(λ₂)= 1

                                     

Таблица 2 – Коэффициент восстановления полного давления воздуха вдоль трубы

		0,84			0,96	1
	0,9518	0,9691	0,9826	0,9923	0,9981	1
	1	0,982	0,968	0,959	0,953	0,9518

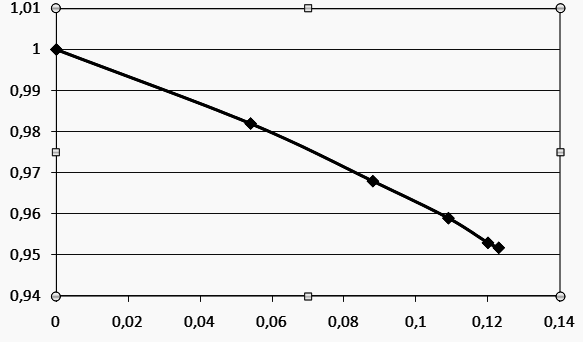
Рисунок 3 – Изменение коэффициента восстановления полного давления воздуха вдоль трубы

3 Исходные данные

Воздух вытекает из бака в атмосферу через сопло Лаваля, соединённое с теплоизолированной трубой, диаметром d=50 мм и длиной l=2м. Давление и температура в баке поддерживаются постоянными и равными  Приведённая скорость на входе в трубу  Определить режим течения в трубе. Найти изменение статического давления по длине трубы. Потерями энергии в сопле пренебречь ().

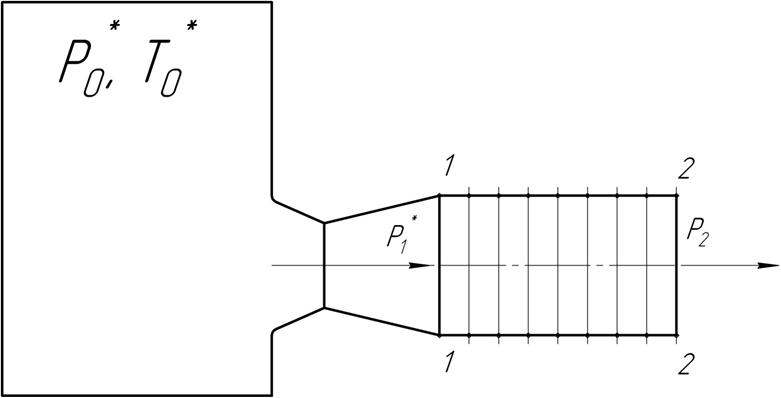
Рисунок 4 – Схема истечения воздуха из бака

  4  Расчет

Из расчетов видно, что , это говорит о том, что внутри трубы есть скачок уплотнения.

4.1 Определение приведенной длины трубы:

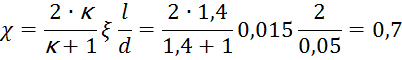
4.2 Критическая приведенная длина трубы (λ₂=1,φ(λ₂)=1):

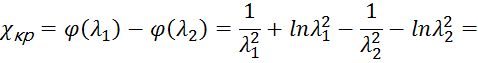
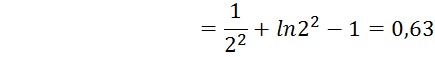
а) Располагаемое отношение давления соответствующее предельным режимам работы, при  .

1-й предельный режим и :

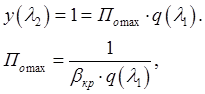
где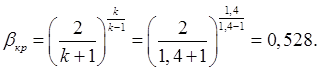

- газодинамическая фунция расхода на входе в трубу.

Имеем:

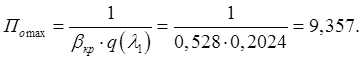
Найдем давление в баке при этом режиме:

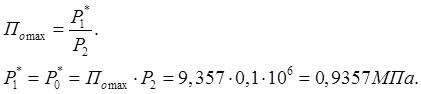
2-й предельный режим скачок уплотнения во входном сечении трубы:

а)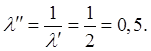

б) Приведенная скорость  на выходе из  трубы :

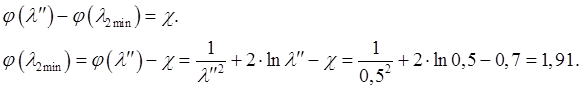
Из графика  зависимости  для дозвуковой части имеем, что

в) Располагаемое отношение давлений соответствующее располагаемому скачку уплотнения во входном сечении трубы :

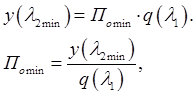
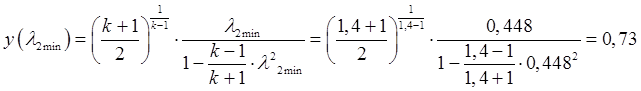
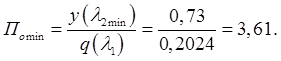
Найдем давление в баке при этом режиме:

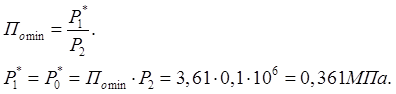
Так как ,  то внутри трубы будет скачок уплотнения.

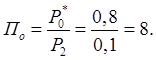
4.3 Определение  приведённой скорости  на входе из трубы

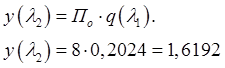
При  по ГДФ 

4.4 Определение местоположения скачка уплотнения:

   Вспомогательная функция :

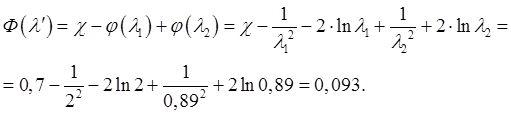
Приведенная скорость перед скачком определяется из графика  зависимости  .

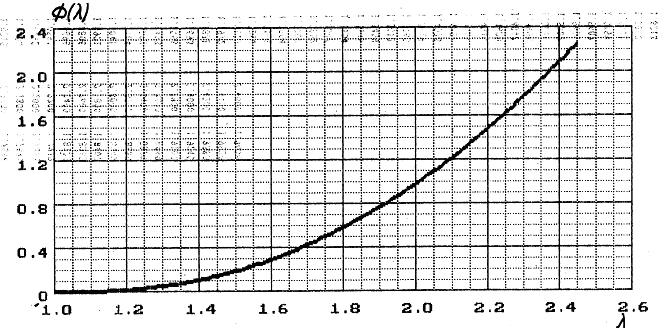
Рисунок 5 - Зависимость

                                                                 

   За скачком уплотнения приведенная скорость  равна:

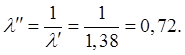
  Расстояние до скачка уплотнения:

Изобразим изменение приведенной скорости и местоположение скачка уплотнения вдоль трубы на рисунке 6.

Таблица 3 – Изменение приведённой скорости вдоль трубы

λ	2	1,8	1,6	1,4	1,38	0,72	0,8	0,89
χ	0	0,153	0,306	0,453	0,467	0,467	0,61	0,7

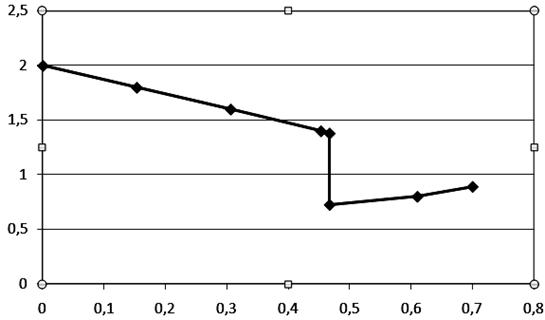
Рисунок 6 – Изменение приведенной скорости вдоль трубы

      4.5 Определение  изменения статического давления по длине трубы:

,

 где -газодинамическая функция температуры.

Определим   вдоль трубы при определенных  :

При  по ГДФ τ(λ₁)=0,3333

При   τ(λ₂)=0,4600

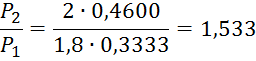
При   τ(λ₂)=0,5733

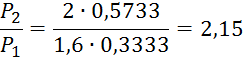
При   τ(λ₂)=0,6733

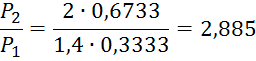
При   τ(λʹ)=0,6826

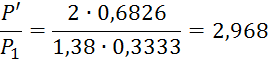
При   τ(λʹʹ)=0,9136

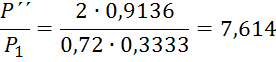
При   τ(λ₂)=0,8933

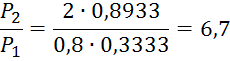
При   τ(λ₂)=0,8680

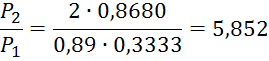
Таблица 3 – Изменение статического давления по длине трубы

λ	2	1,8	1,6	1,4	1,38	0,72	0,8	0,89
χ	0	0,153	0,306	0,453	0,467	0,467	0,61	0,7
	1	1,533	2,15	2,885	2,968	7,614	6,7	5,852

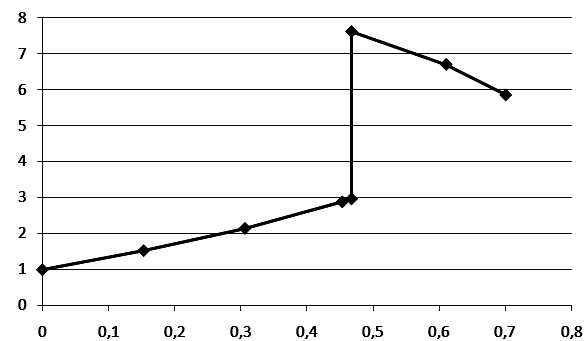
Рисунок 7 – Изменение статического давления по длине трубы