Задача №2
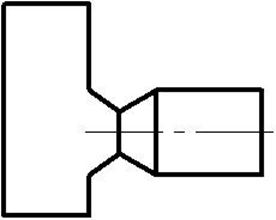
Воздух вытекает из бака в атмосферу через сопло
Лаваля, соединенное с теплоизолированной трубой. Давление и температура в баке
поддерживается постоянными и равными ![]() ,
, ![]() . Приведенная скорость на входе в
трубу
. Приведенная скорость на входе в
трубу ![]() . Определить режим течения в трубе.
Найти приведенную длину трубы, изменение по длине трубы приведенной скорости и
отношение статического давления воздуха в трубе к статическому давлению воздуха
во входном сечении трубы. Потерями энергии в сопле пренебречь
. Определить режим течения в трубе.
Найти приведенную длину трубы, изменение по длине трубы приведенной скорости и
отношение статического давления воздуха в трубе к статическому давлению воздуха
во входном сечении трубы. Потерями энергии в сопле пренебречь ![]() .
.
Принимаем,
что давление на выходе из трубы равно атмосферному, ![]() .
.
Решение
 1. Система уравнений для адиабатного течения газа с трением в трубе
постоянного сечения:
1. Система уравнений для адиабатного течения газа с трением в трубе
постоянного сечения:
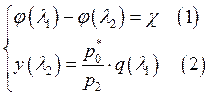 ,
,
где
![]() вспомогательная функция, равна:
вспомогательная функция, равна:
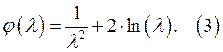
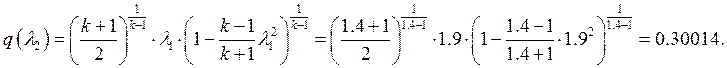
Газодинамическая функция, из (2):
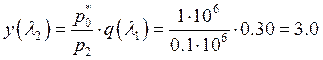 .
.
По
таблицам газодинамических функций по посчитанному значению ![]() находим значение приведённой
скорости:
находим значение приведённой
скорости:
|
|
|
|
1.33 |
2.9780 |
|
1.34 |
3.0164 |
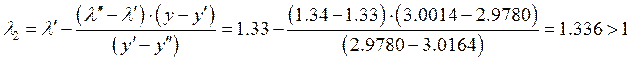 .
.
Течение в трубе сверхзвуковое.
2. Приведённая длина трубы определяется с учётом уравнений (1) и (3):
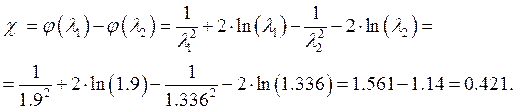
3.
Изменение приведённой скорости вдоль трубы. Для этого разобьём интервал ![]() на
на ![]() частей
с шагом
частей
с шагом ![]() . Используя (1) и (3) находим
приведённую длину
. Используя (1) и (3) находим
приведённую длину ![]() . Полученный результат
приведён в табл. 1. График зависимости изменения приведённой скорости по длине
трубы представлен на рис. 2.
. Полученный результат
приведён в табл. 1. График зависимости изменения приведённой скорости по длине
трубы представлен на рис. 2.
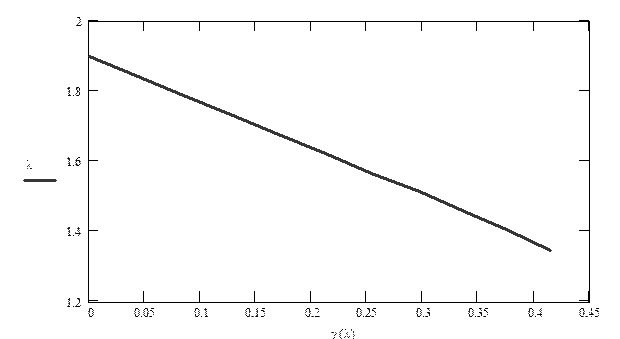
Рис. 2 – Изменение приведённой скорости вдоль трубы.
4. Изменение отношения статических давлений вдоль трубы. Связь между статическими давлениями:
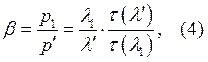
где
![]() статическое давление вдоль трубы;
статическое давление вдоль трубы;
![]() газодинамическая функция
температуры:
газодинамическая функция
температуры:
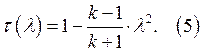 .
.
Для
построения зависимости разобьём интервал ![]() на
на
![]() частей с шагом
частей с шагом ![]() . Для нахождения используем (4) и
(5). Полученный результат приведён в таблице 1. График зависимости изменения
отношения статического давления вдоль трубы приведён на рис. 2.
. Для нахождения используем (4) и
(5). Полученный результат приведён в таблице 1. График зависимости изменения
отношения статического давления вдоль трубы приведён на рис. 2.
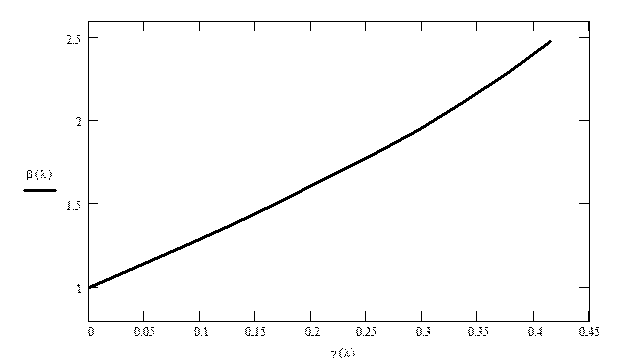
Рис. 3 – Изменение отношения давлений вдоль трубы.
5. Результаты расчёта.
Табл. 1 – Результаты расчёта.
|
|
|
|
|
|
|
1.9 |
1.561 |
0 |
0.398 |
1 |
|
1.844 |
1.518 |
0.043 |
0.434 |
1.122 |
|
1.787 |
1.474 |
0.086 |
0.468 |
1.248 |
|
1.731 |
1.431 |
0.13 |
0.501 |
1.38 |
|
1.674 |
1.388 |
0.173 |
0.533 |
1.518 |
|
1.618 |
1.344 |
0.216 |
0.564 |
1.662 |
|
1.562 |
1.301 |
0.259 |
0.594 |
1.813 |
|
1.505 |
1.259 |
0.301 |
0.622 |
1.972 |
|
1.449 |
1.218 |
0.343 |
0.65 |
2.141 |
|
1.392 |
1.178 |
0.383 |
0.677 |
2.319 |
|
1.336 |
1.14 |
0.421 |
0.703 |
2.508 |
Пример
расчета при ![]() .
.
Приведённая длина трубы определяется с учётом уравнений (1) и (3):
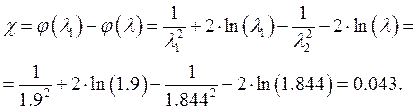
Изменение отношения давлений вдоль трубы определяем по формуле (4):
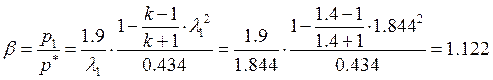 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.