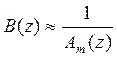Другие предметы \ Агротехника

Постановка задачи селекции. Спектральные методы решения задачи. Описание метода эксперимента и полученных результатов, страница 6

, где Am(z) – системная функция АР-процесса, который аппроксимирует процесс B(z). Тогда, определив по (3.8) АР-параметры модели A(z), можно выразить полином B(z):

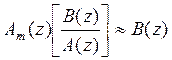,                                                    (3.9)

где 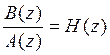 - системная функция рассматриваемого АРСС-процесса, представляющего собой запись экспериментальных данных.

Таким образом, процесс определения параметров АРСС-модели можно разделить на следующие этапы:

1)  сбор данных и синтез исходной временной последовательности xn;

2)  формирование АКП исходного процесса;

3)  нахождение АР-параметров модели;

4)  фильтрация последовательности xn фильтром на основе найденных АР-параметров и выделение остаточных ошибок фильтрации полинома B(z);

5)  аппроксимация АР-моделью остаточных ошибок фильтрации;

6)  оценивание через обратное z-преобразование СС-параметров.

СПМ   в диапазоне относительных частот  получаем масштабированием интервалом отсчетов T:

.

Тогда критерий качество СКО имеет вид:

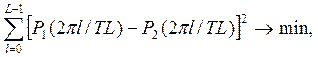
где L – количество спектральных отсчетов;

,  - СПМ контрольного спектра и исследуемой АРСС-модели.

Достаточность порядка контрольной модели выражается в асимптотическом стремлении отклонений контрольных спектров соседних порядков к величинам, не превышающим уровня обычных флюктуаций исследуемых реализаций.

  4. Описание метода эксперимента и полученных результатов.

При проведении экспериментов были использованы последовательности отсчетов, полученные при помощи следующей схемы измерения (рис 4.1). При возникновении однофазного замыкания в кабельной сети с изолированной нейтралью изменяются емкостные составляющие тока на землю, что приводит к нарушению баланса токов в поврежденной линии. При этом появляется сигнал с измерительного трансформатора (ток нулевой последовательности).

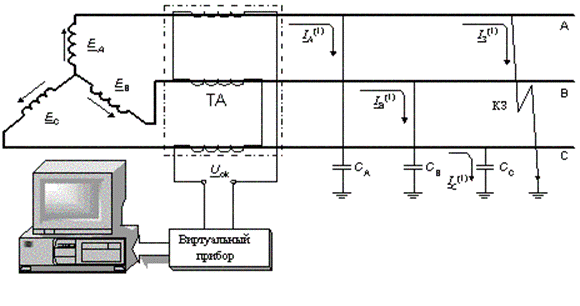
рис 4.1 Схема измерения ТНП.

  Имеется  четыре файла с отсчётами ТНП: UA, UB, UC, 3U0. UA, UB, UC – токи в каждой из фаз (A, B, C); 3U0 – суммарный ток фаз. С точки зрения анализа, токи в каждой из фаз оказались наименее информативными, поэтому наиболее подробному исследованию подвергся файл 3U0. Форма тока показана на рис. 4.2.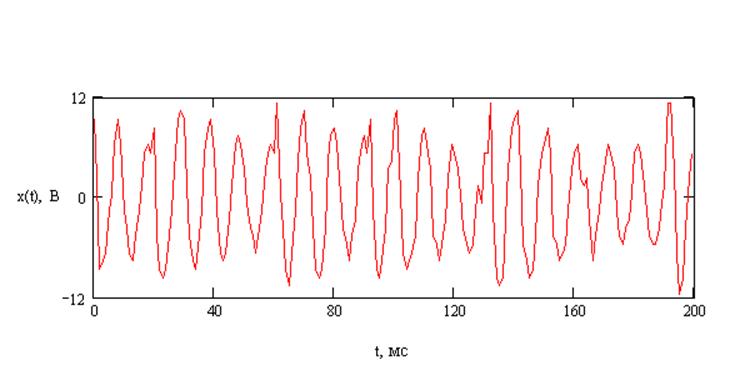

Рис. 4.2 Форма тока в измерительной цепи при ОЗЗ.

Как было указано выше, наличие в сети ДГР сильно осложняет селекцию ОЗЗ, поэтому исследуемая последовательность была подвергнута фильтрации на частоте 50 Гц, чтобы максимально приблизить условия эксперимента к реальным. Частота дискретизации выбрана 1000 Гц, что позволяет анализировать гармоники вплоть до 10.

По принятым представлениям в спектре ТНП присутствуют все гармоники частоты 50 Гц, однако при определённых условиях (одинаковое напряжение зажигания дуги для отрицательной и положительной полуволн), 2, 4, ..(2n) гармоники могут отсутствовать [1]. Первым этапом обработки данных было построение спектра ТНП при помощи преобразования Фурье рис. 5.1. На рисунке чётко виден доминантный пик на частоте 100 Гц и постоянная составляющая. Остальные составные части спектра скрываются шумами и не видны чётко даже после применения процедуры взвешивания последовательности окном Натолла (рис. 5.2) с параметрами а0= 0,3635819, а1= 0.4891775, а2= 0.1365995, а3= 0.0106411  [2]. Моделирование исходного процесса АР-фильтром, дало аналогичный результат (рис. 5.3).

Для того чтобы увидеть тонкую структуру спектра были выполнены рекомендации из [2] и [3], а именно удаление математического ожидания и предварительное выбеливание (в [3] эта процедура называется prewhitening). Данные процедуры фильтрации (удаление математического ожидания, АРСС-фильтр) гарантируют стационарность фильтрованной последовательности, как того требует теория моделирования передаточной функции.

Скачать файл