К параметрическому описанию статистик второго порядка можно прийти, рассматривая модель временного ряда, соответствующего анализируемому временному процессу. В этом случае СПМ модели временного ряда будет, прежде всего, некоторой функцией от параметров этой модели, а не АКП. Одна из причин применения параметрических моделей обусловлена возможностью получения на основе этих моделей более точных оценок СПМ, чем это возможно с помощью классических методов спектрального оценивания.
Рассмотрим применение коррелограммного метода спектрального анализа [7]. Предположим, что данный процесс xn является стационарным в широком смысле, действительным дискретным стохастическим процессом с нулевым математическим ожиданием. Тогда СПМ представляет собой распределение мощности по частотам и определяется, согласно теореме Винера-Хинчина как ДПФ от автокорреляционной функции:
,
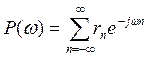(3.1)
где rn – отсчёты корреляционной функции.
Коррелограммный метод спектрального оценивания заключается в расчёте согласно (3.1), но по конечной последовательности оценок АКП вместо бесконечной последовательности неизвестных истинных значений:
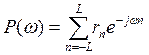, (3.2)
где rn – несмещённые оценки АКП:
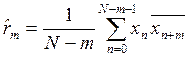
(3.3)
Максимальный индекс временного сдвига p как правило намного меньше длины последовательности данных N, что обусловлено недостаточной точностью оценки высоких порядков автокорреляции при конечной длине реализаций. С увеличением числа значений оценки автокорреляции, коррелограммный метод дает асимптотические несмещенные оценки СПМ.
Перейдем к рассмотрению периодограммного метода спектрального оценивания [2]. Полагая исследуемый процесс эргодичным, периодограммные оценки СПМ можно получить следующим образом:
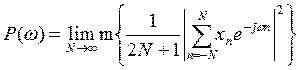(3.4)
Пренебрегая
операцией вычисления математического ожидания m[.] и
полагая, что конечное множество данных 
содержит
N отсчетов, получаем выборочный спектр:
,
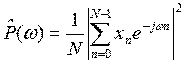(3.5)
являющийся исходной немодифицированной формой периодограммной оценки СПМ. Выборочный спектр будет давать статистически несостоятельные оценки, поскольку была опущена операция вычисления математического ожидания, предусмотренная в (3.4). Поэтому для сглаживания периодограммы необходимо применять что-то вроде псевдоусреднения по ансамблю. Предложены три основные метода сглаживания.
В методе Даньелла периодограмма сглаживается путём усреднения по соседним ячейкам частотного разрешения:
.
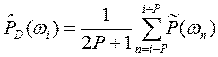Сглаживание по методу Бартлетта основано на создании псевдоансамбля
периодограмм за счет деления последовательности из N
отсчетов данных на P неперекрывающихся
сегментов по D отсчётов в каждом, так что 
. По каждому сегменту независимо
вычисляется выборочный спектр в диапазоне -1/2T<f<1/2T:
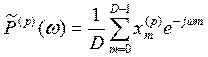
для чего может быть использован алгоритм ДПФ на некоторой сетке частот. Затем на каждой частоте, представляющей интерес, P отдельных немодифицированных периодограмм усредняются, с тем, чтобы получить усредненную периодограмму Бартлетта. Устойчивость данной спектральной оценки улучшается как величина, обратная числу сегментов. Разрешение в результате разбиения данных на сегменты будет ухудшаться, так как смещение спектральной оценки каждого из сегментов будет определяться воздействием окна, главный лепесток которого с уменьшением длины сегмента будет расширяться.
Сглаживание по методу Уэлча производится путем применения подхода Бартлетта к перекрывающимся сегментам, а также вводится окно данных для каждого сегмента. Перекрытие сегментов позволяет более полно использовать данные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.