Постановка задачи селекции. Спектральные методы решения задачи. Описание метода эксперимента и полученных результатов, страница 5

Несколько слов следует сказать о применении весовых окон данных. Основное назначение окна данных – уменьшить величину смещения в спектральных оценках. При этом имеющуюся конечную запись данных удобно рассматривать как некоторую часть соответствующей бесконечной последовательности, видимой через используемое окно. Преобразование финитной наблюдаемой последовательности, таким образом, является искажённой версией преобразования бесконечной. Минимальная ширина спектральных пиков взвешенной окном последовательности будет определяться главным лепестком преобразования окна, и не будет зависеть от исходных данных. Боковые лепестки будут вносить искажения в амплитудную картину спектра. Это явление, возникающее из-за конечности обрабатываемых записей называют просачиванием или размыванием (эффект Гиббса). Окна представляют собой весовые функции, предназначенные для уменьшения этого эффекта. Для уменьшения последствий спектрального просачивания амплитуда боковых лепестков относительно главного должна быть малой, а переход от главного лепестка к боковым максимально быстрым. Известен ряд функций окна, применение которых позволяет снизить уровень боковых лепестков, однако при этом основной лепесток расширяется; поэтому выбор параметров окна является результатом компромисса между уменьшением смещения и требуемым спектральным разрешением.

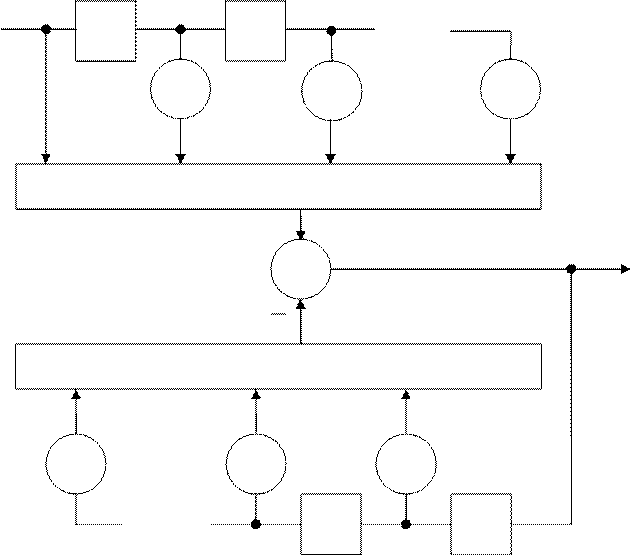
Модельный подход, как было указанно выше, является альтернативой непараметрическим методам спектрального оценивания. Частным классом параметрических моделей является модель процесса АРСС. На рис. 3.1 приведена соответствующая модель временного ряда,

 

x_nZ^-1                         Z^-1                        .   .   .

b₁                           b₂                                b_q

                                                                     +

                                                               y_n

 

a₁                                                 a₂                                        a_p

                                           .   .   .

Z^-1                         Z^-1

Рис. 3.1 Фильтр авторегрессии-скользящего среднего порядка (p,q)

представляющая собой фильтр АРСС порядка (p,q). Выходные процессы моделей этого класса имеют спектральные плотности мощности, которые полностью описываются с помощью параметров модели и дисперсии белого шумового процесса. Значения этих параметров и дисперсия белого шума определяются по АКП. АРСС-модель имеет физический смысл, т.к. является дискретным аналогом хорошо известного линейного дифференциального (или для данного случая линейного разностного) уравнения, используемого для описания линейных систем [6]:

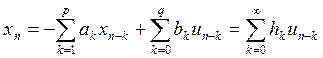 ,                                (3.6)

где u_k – входная возбуждающая последовательность;

a_k, b_k, h_k – коэффициенты полиномов A(z), B(z), H(z), которые имеют вид [6]:

.

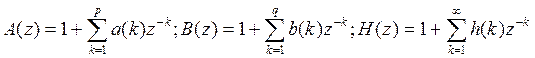Возбуждающая последовательность представляет собой белый шум с нулевым средним и дисперсией [2]. Коэффициенты полинома A(z), представляющие собой параметры авторегрессионной составляющей АРСС-модели можно найти решая нормальное уравнение Юла-Уолкера [2]:

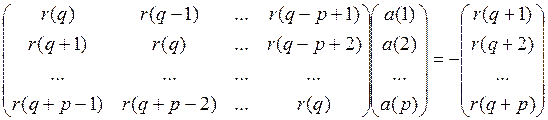,                (3.7)

где r(i) – коэффициенты АКП исследуемого процесса. Значения параметров СС-составляющей (коэффициенты полинома B(z)) не являются решениями линейной системы уравнений. Поэтому для моделирования часто принимают q=0, а АР параметры находят из выражения:

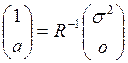,                                                               (3.8)

где a – p-мерный вектор-столбец АР-параметров, R – корреляционная матрица исследуемого процесса вида (3.7) при условии q=0, o – p-мерный нулевой вектор-столбец.

Следует отметить, что возможно найти приближенные значения СС-параметров, решая линейные системы уравнений [2], [6]. Сущность подхода заключается в аппроксимации СС-составляющей моделирующего фильтра избранного порядка q, АР-моделью большего порядка m (m>q). Положим, что: