Расчёт панелей из композиционных материалов, страница 7

На основании вышесказанного предлагается следующий алгоритм расчета:

1. Исходные данные:

Модули Юнга монослоя по основе Е₁ и по утку Е₂;

Модуль сдвига G₁₂;

Коэффициент Пуассона  μ₁₂;

Углы укладки слоев φ_k ;

Пределы прочности монослоев  на растяжение по основе и по утку и на сжатие по основе и по утку соответственно;

Толщина монослоя:

2. Определяются коэффициенты Q_ij для каждого слоя согласно (19.8) или (19.10) в зависимости от требуемой степени точности расчета.

3.  Вычисляем коэффициенты  в общей системе координат по (19.12) для каждого слоя.

4.  Определяем положение нейтрального слоя по следующей зависимости:

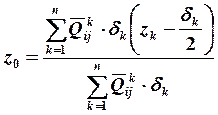                                                              (19.16)

где 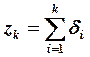 - расстояние от края пакета до (k + 1) слоя;

δ_k – толщина k – го слоя.

Если укладка симметричная, то положение нейтрального слоя совпадает со срединной поверхностью h/2.

5.  Находим коэффициенты матрицы жесткости системы А_ij, В_ij, D_ij по выражениям (19.5), (19.6), (19.7) соответственно.

6.  На этом этапе можно определить модули Юнга всей системы Е_х,  Е_у , коэффициенты Пуассона μ_хуи модуль сдвига G_ху по следующим формулам:

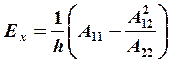                                                  (19.17)

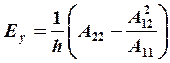                                                  (19.18)

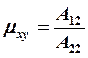;    (19.19),  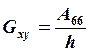                           (19.20)

7. Из выражения (19.15) находим деформации

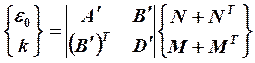                                    (19,21)

Для этого необходимо обратить матрицу жесткости. Обращенная матрица жесткости называется матрицей податливости. Или же систему уравнений (19.15) решить относительно неизвестных деформаций ε и k, например, методом Гаусса.

Если укладка симметричная, то коэффициенты матрицы В равны 0 и если на пластину не действуют моменты М_х, М_у, М_ху то

                                                    (19.22)

В этом случае составляющие матрицы податливости а_ij в развёрнутом виде определяются по следующим зависимостям:

;   ;

;   ;

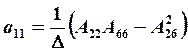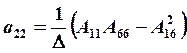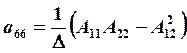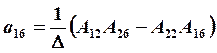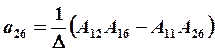;   где

     (19.24)

8. Определяем полные деформации в каждом слое по формулам:

                                        (19.25)

В развёрнутом виде выражение выглядит следующим образом:

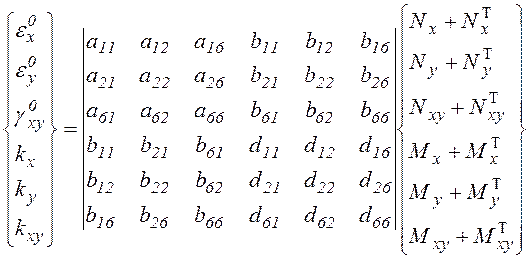         (19.26)

Подставив в (6.25) значения  и k получим ,  и

(19.27)

(19.28)

(19.29)

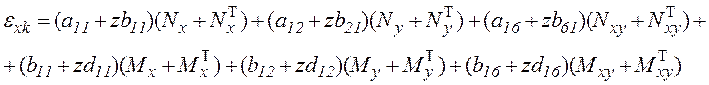
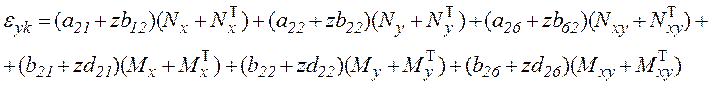
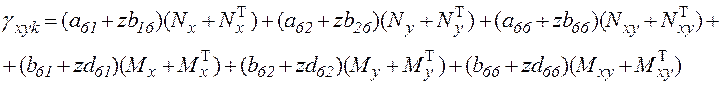
1.  Напряжения в осях х и у для каждого слоя определяем используя закон Гука:

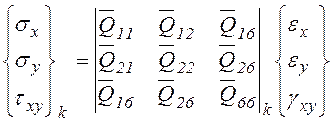                                     (19.30)

2.  Напряжения в направлениях упругой симметрии т.е. в направлении основы  и утка вычисляем по следующим зависимостям:

               (19.31)

               (19.32)

             (19.33)

3.  Определяем запасы прочности по критерию Хилла-Мизеса.

                                                     (19.34)                               где, F₁, F₂, и F₁₂ – пределы прочности

Если напряжения  и (или)  - сжимающие, то , , если  и (или)  - растягивающие, то , .

 разрушающее.

Примечание:

На основании приведенного материала выполняется  расчётно-проектировочная работа (РПР) по теме «Расчёт пластин из композиционных материалов».

В сборнике лекций Е.Матвеева есть дополнительный материал по КМ, расчёт пластинок из КМ. См. файл «Прочность конструкций из КМ». От 11.04.2010.

Рекомендуется дополнительный материал из учебного пособия КуАИ:

УДК 539.3: 629.7.023

Авт. Леонов В.И. «Расчёт элементов авиаконструкций типа ортотропных и трёхслойных пластин». Учебное пособие. – Куйбышев: КуАИ. 1983, с. 62.

(В учебном пособии излагается теория тонких ортотропных пластин с лёгким заполнителем. Даётся вывод дифференциальных уравнений продольно-поперечного изгиба, и рассматриваются методы решения задач изгиба и устойчивости пластин).