Расчёт панелей из композиционных материалов, страница 5

σ₂ = с₂₁ε₁ + с₂₂ε₂ + с₂₃ε₃ + с₂₄ε₄ + с₂₅ε₅ + с₂₆ε₆

σ₃ = с₃₁ε₁ + с₃₂ε₂ + с₃₃ε₃ + с₃₄ε₄ + с₃₅ε₅ + с₃₆ε₆                                    (17.4)

………………………………………………..

………………………………………………..

σ₆ = с₆₁ε₁ + с₆₂ε₂ + с₆₃ε₃ + с₆₄ε₄ + с₆₅ε₅ + с₆₆ε₆

Заметим, что для ортотропных материалов (имеющих три взаимно ортогональные плоскости симметрии упругих свойств), коэффициенты с₁₄, с₁₅, с₁₆, с₂₄, с₂₅, с₂₆, с₃₄, с₃₅, с₃₆, с₄₁, с₄₂, с₄₃, с₄₅, с₄₆, с₃₄, с₅₁, с₅₂, с₅₃, с₅₄,  с₅₆, с₆₁, с₆₂, с₆₃, с₆₄, с₆₅ = 0.

Исходя из этого матрица с_ij запишется следующим образом:

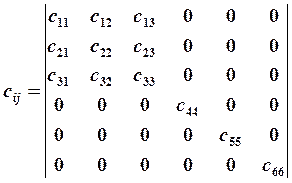
                                                (17.5)

Тогда уравнение (17.2) с учётом (17.5) в развёрнутой форме запишется:

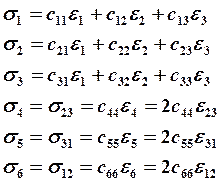                                                       (17.6).5)

Уравнения (17.6) можно обратить с помощью стандартных матричных преобразований:

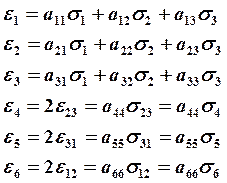                                                    (17.7).6)

Матрица коэффициентов а_ij  называется матрицей податливости и является транспонированной матрицей алгебраических дополнений элементов матрицы с_ij.

                                                            (17.8)

18. Слои композитных материалов

Основной элемент в большинстве композитных изделий, армированных длинными волокнами, это слой из волокон и матрицы. Причём все волокна ориентированы в одном направлении, что осуществляется послойным выкладыванием препрега.

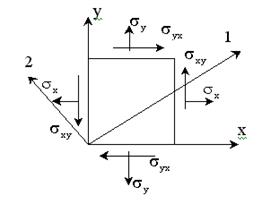Рассмотрим небольшой элемент слоя с постоянной толщиной.

Главные оси материала («основа» и «уток») направлены по осям 1 и 2. Оси х и у являются осями произвольной системы координат. Условия равновесия, связывающие напряжения σ_х, σ_у, σ_ху и σ₁, σ₂, σ₁₂  (σ_ху  и σ₁₂ являются касательными напряжениями и иногда обозначаются, как τ_ху и τ₁₂  соответственно) позволяют получить следующую зависимость:

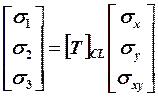
     (18.1)

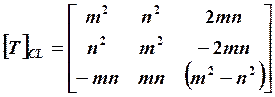    (18.2)

m = Cos θ , n = Sin θ.

Индексы CL соответствуют двумерному случаю, т.е. в плоскости 1-2 или х-у.

Аналогично определяется и соотношения между деформациями

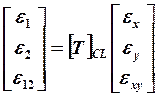                                                                                         (18.3)

Эти уравнения не учитывают поперечных сдвиговых деформаций. Учет влияния поперечной сдвиговой деформации приводит к появлению соотношений σ₄ – ε₄ и σ₅ – ε₅. Это обстоятельство должно учитываться при анализе термического расширения, так как в направлении волокон механические свойства определяются свойствами волокна. А в направлении толщины преобладающее влияние может оказывать материал матрицы.

 (18.4),  (18.5), 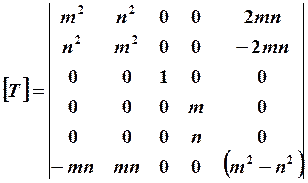  (18.6)

Если воспользоваться законом Гука, связывающего напряжения и деформации, а также свойствами симметрии, кроме того, учесть влияние термических воздействий, то можно получить зависимость для описания поведения композитных материалов в осях 1 – 2.

Экскурс в сопромат

Напряжённое состояние тела будет определено, если будут найдены шесть компонентов напряжённого состояния σ_х,  σ_у,  σ_z,  τ_х,  τ_у,  τ_z  в каждой точке, компоненты деформации в данной точке тела ε_х,  ε_у,  ε_z,  γ_ху,  γ_уz,  γ_zx, они будут непрерывными функциями координат во всём объёме тела. Между компонентами напряжённого состояния и компонентами деформации в данной точке существуют зависимости, называемые обобщённым законом  Гука. Его вид

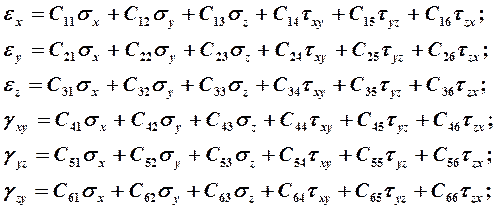        (18.*)

где  для однородного материала коэффициенты С_ij – постоянные, зависящие от материала.

Для изотропного материала уравнения обобщённого закона Гука запишутся в виде

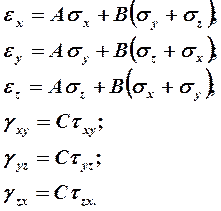   (18.**)  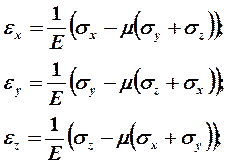       (18.***)

Постоянные величины А, В, С, входящие в уравнения (18.**), выражаются через две упругие константы изотропного материала, определяемые для каждого материала экспериментально.

Второй вид выражения закона Гука в перемещениях от воздействия внешних сил и температурного воздействия:

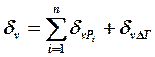,  где  δ_vi  и δ_vT  - коэффициенты, зависящие от выбранного направления в точке, от материала и геометрии тела соответственно, зависящие от законов распределения сил и температуры и не зависящие от их величин .

Переходя к рассмотрению свойств КМ с точки зрения закона Гука, можно вывести зависимость

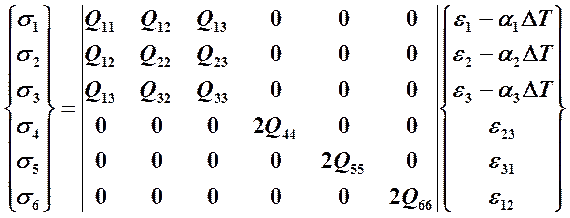        (18.7)